lecksuchtechnik.de

Die viskose Strömung

Gasmoleküle verhalten sich bei Drücken oberhalb von ungefähr 0,01 mbar ähnlich wie Flüssigkeiten. Die Moleküle sind so eng beieinander, dass sie ständig gegeneinander stoßen. Werden sie gepumpt oder herrscht eine Druckdifferenz, so strömen sie gemeinsam.

Bei der viskosen Gasströmung unterscheiden wir zwei Arten:

a.) Die turbulente Strömung, und

b.) die laminare Strömung.

Zur Abschätzung, welche Strömungsart in einem Leck zu erwarten ist, kann die folgende Tabelle dienen:

Strömungsart

turbulent

laminar

Übergangsströmung

molekular

Leckrate (mbar · l/s)

〉 10^-2

10^-1 - 10^-6

10^-4 - 10-7

〈 10^-7

Tabelle 9
Quelle: Leakage Testing Handbook, Prepared for Liquid Propulsion Section, Jet Propulsion Laboratory, National Aeronautics and Space Administration, Pasadena, California)

In der Lecksuchtechnik ist man meistens auf das Abschätzen der Strömungsart angewiesen. Es gibt natürlich Formeln zur Berechnung des Leitwertes für verschieden geformte Rohre etc. Alle diese Formeln enthalten Geometriefaktoren (Länge, Durchmesser etc.). Da bei Leckagen die Geometrie des Lecks in den meisten Fällen unbekannt ist, nützen die erwähnten Formeln nicht.

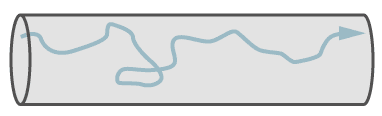
Die turbulente Strömung

Die turbulente Strömung ist eine verwirbelte Strömung. Sie tritt nur bei größeren Lecks auf und eher bei höheren Drucken. Ebenfalls ist eine hohe Geschwindigkeit des Gasstromes erforderlich. Nur Lecks mit turbulenter Gasströmung "pfeifen" und können deshalb per Schall oder Ultraschall geortet werden.

Die Formel für die Leckrate bei turbulenter Strömung wird hier nicht extra aufgeführt. Lecks mit turbulenter Strömung sind ohnehin zu groß. Sie müssen geortet und beseitigt werden und werden nur selten einer Berechnung unterzogen.

Die laminare Strömung

Die laminare Strömung wird definiert als parallele Strömung in einem Rohr, wobei die Verteilung der Geschwindigkeit der Moleküle parabolisch ist.

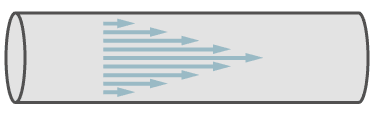
In der gezeigten Abbildung symbolisieren die Länge der Pfeile die Geschwindigkeit der Moleküle. Die bekannteste Formel für die laminare Gasströmung stammt von Poisseuille. Sie beschreibt die laminare Strömung durch ein grades Rohr mit rundem Querschnitt:

Die folgend gezeigte Formel von Poisseuille zeigt den Zusammenhang der Komponenten für die Leckrate bei laminarer Strömung.

$q = \frac{\pi \cdot r^4}{16 \cdot \eta \cdot l} \, ({p_1}^2 - {p_2}^2)$

$\eta = \textup {dynamische Viskosität des Gases}$

$l = \textup {Länge des runden Rohres (Kapillare)}$

$r = \textup {Radius der Kapillare}$

$p_1 = \textup {der h\"ohere Druck}$

$p_2 = \textup {der niedrigere Druck}$

Wenn man annimmt, dass die geometrischen Abmessungen eines Lecks, die ja meistens unbekannt sind, sich während des Zeitraums einer oder mehrerer Messungen nicht ändert, so kann man die Konstanten und die Geometriefaktoren zu einem Faktor K zusammenfassen:

$q = K \, \frac {({p_1}^2-{p_2}^2)}{\eta}$

Wobei K aus den folgenden Konstanten besteht:

$K = \, \frac {\pi \cdot r^4}{16 \cdot l}$

Wenn sich bei gleichbleibender Gasart der Differenzdruck über einem Leck ändert, so ändert sich die Leckagerate quadratisch zum Druck nach der folgenden Formel:

$\frac{q_A}{({p_{A1}}^2-{p_{A2}}^2)} = \frac{q_B}{({p_{B1}}^2-{p_{B2}}^2)}$

Man kann also durch Erhöhen der Druckdifferenz bei einer Dichtheitsprüfung die Leckrate quadratisch zum Druck erhöhen und damit eine starke Empfindlichkeitssteigerung erreichen. Bei großen Behältern, die z.B. für einen Schnüffeltest mit einem Spürgas gefüllt werden müssen, kann man eventuell Kosten sparen, indem man den Druck erhöht, aber mit einem geringeren Prozentsatz des Spürgases arbeitet. Natürlich müssen dabei die drucktechnischen Sicherheitsvorschriften beachtet werden.

Beispielberechnung

Ein interessantes Beispiel sei hier einmal berechnet, nämlich der Unterschied in der Leckrate beim Schnüffeltest und beim Vakuumtest. Die Leckgeometrie und die Gasart bleiben unverändert, ebenfalls ist der Differenzdruck über dem Leck beide Male 1 bar. Der Unterschied besteht nur darin, dass beim Vakuumtest 1 bar gegen Null bar und beim Schnüffeltest 2 bar gegen 1 bar (absolut) herrschen.

Vakuumtest

$q_A = 5 \cdot 10^{-5} \, {\textup{mbar l} \over s }$

$p_{A1} = 1 \, bar$

$p_{A2} = 0 \, bar$

Schnüffeltest

$q_{B} = \, ?$

$p_{B1} = 2 \, bar$

$p_{B2} = 1 \, bar$

Die Leckrate ist beim Schnüffeltest also drei mal größer als beim Vakuumtest, obwohl dem ersten Anschein nach der gleiche Differenzdruck vorhanden ist.

Wenn sich die Gasart ändert, so ändert sich die Leckrate umgekehrt proportional zur Viskosität der Gase.

Viskosität einiger bekannter Gase

Gasart

Luft

Stickstoff

Sauerstoff

Argon

Helium

R-12

R-22

R-134a

R-600a

Formel

N₂

O₂

CCl₂F₂

CHClF₂

CH₂F-CF₃

CH(CH₃)₂-CH₃

Viskosität bei 15°C
in Pa·s

18,0 · 10^-6

16,3 · 10^-6

19,9 · 10^-6

22,0 · 10^-6

19,2 · 10^-6

11,6 · 10^-6

12,0 · 10^-6

11,61 · 10^-6

7,4 · 10^-6

Tabelle 10

Umrechnung von Helium-Leckrate bei laminarer Strömung auf andere Gase

Umrechnen auf:

q von Argon

q von Neon

q von Wasserstoff

q von Stickstoff

q von Luft

q von Wasserdampf

Multipliziere Heliumleckrate mit:

0,883

0,626

2,23

1,12

1,08

2,09

Tabelle 11

Wie man aus dieser Tabelle erkennen kann, ist bei laminarer Strömung der Unterschied in der Leckrate zwischen den Gasen Helium und Luft nur 8 %, kleiner also als die Messgenauigkeit von Heliumlecksuchgeräten. Deshalb ist es erlaubt, wohlbemerkt bei laminarer Strömung, wenn mit einem Luft-Heliumgemisch gesucht wird, die Luft- Leckrate gleich der Helium-Leckrate zu setzen. Wenn man mit einem Helium-Luftgemisch mit 10 % Heliumgehalt arbeitet, so darf man sagen, die angezeigte Leckrate ist 10 % von der Gesamt-Leckrate.

Molekulare Strömung

Molekulare Strömung herrscht bei kleinen Leckagen (siehe Tabelle 9) und bei niedrigen Drücken. Bei molekularer Strömung wandert jedes Molekül unabhängig von anderen Molekülen. Die mittlere freie Weglänge ist größer als der Durchmesser der Leckkapillare. Damit ist es möglich, dass ein einzelnes Molekül auch gegen das Druckgefälle und die allgemeine Strömungsrichtung wandert, da sich ja die Moleküle nicht berühren, sondern nur mit den Wandungen zusammenstoßen. Trotz dieser Möglichkeit des Gegenströmens erfolgt der Gesamtfluss in Richtung des Druckgefälles. Bei molekularer Strömung fließen die Moleküle in Richtung des Partialdruckgefälles.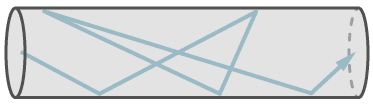

Die Formel von Knudsen für die Leckrate bei molekularer Strömung lautet:

$q=\frac {\sqrt{2\pi}}{ 6 } \sqrt { \frac { R\cdot T }{ M } } \frac { { d }^{ 3 } }{ l } \left( { p }_{ 1 }-{ p }_{ 2 } \right)$

$\textup {R = allgemeine Gaskonstante}$

$\textup {T = absolute Temperatur(K)}$

$\textup {M = relative Molekülmasse (molare Masse)}$

$\textup {p1 = der h\"ohere Druck}$

$\textup {p2 = der niedrigere Druck}$

$\textup {d = Durchmesser der Leckage}$

$\textup {l = Länge der Leckage}$

Aus der Formel von Knudsen kann man erkennen, dass, im Gegensatz zur laminaren Strömung, bei der molekularen Strömung sich die Leckrate in Abhängigkeit vom Druck linear proportional verändert. Zur Umrechnung der Leckrate bei verändertem Differenzdruck gilt also:

$\frac{q_A}{(P_{A1} - P_{A2})} = \frac{q_B}{(P_{B1} - P_{B2})}$

Die Abhängigkeit der Leckrate bei Änderung der Gasart folgt bei molekularer Strömung reziprok proportional der Quadratwurzel aus der relativen Molekülmasse (molare Masse). Im Gegensatz zur laminaren Strömung kann es hier größere Unterschiede in der Leckrate geben. Die Umrechnung erfolgt (bei gleichbleibendem Differenzdruck) wie in der nächsten Formel gezeigt:

$\frac{q_A}{q_B} = \frac{\sqrt{M_B}}{\sqrt{M_A}}$

Für die Umrechnung von Helium-Leckrate in Luft-Leckrate ergibt sich zum Beispiel:

$\textup {Heliumleckrate} \, q_A = 1 \cdot 10^{-8} \, {mbar \cdot l \over s}$

$\textup {relative Molek\"ulmasse Helium} = \, 4 \, {g \over mol}$

$\textup {relative Molek\"ulmasse Luft} = \, 29 \, {g \over mol}$

$\textup {Luft-Leckrate} \, q_B = \, ?$

$q_B = \frac{q_A \cdot \sqrt{M_A}}{\sqrt{M_B}} = \frac{1 \cdot 10^{-8} \, {mbar \cdot l \over s} \cdot \sqrt{4 \, {g \over mol}}}{\sqrt{29{g \over mol}}} = 3,7 \cdot 10^{-9} \, {mbar \cdot l \over s}$

Die Luftleckrate ist also bei molekularer Strömung rund 2,7 mal kleiner als die Heliumleckrate. Auf Datenblättern von Heliumlecksuchgeräten findet man noch oft, neben der Angabe der kleinsten, nachweisbaren Helium- Leckrate, die Angabe der dazu äquivalenten Luft-Leckrate, die dann um den Faktor 2,7 kleiner ist. Dies kann zu Irrtümern führen, da dieser Umrechnungsfaktor nur für die molekulare Strömung und nicht für den gesamten Messbereich des Lecksuchgerätes gilt. Helium-Lecksuchgeräte der heutigen Generation können auch millionenfach größere Leckraten messen.

Umrechnung von Gewichts-Leckrate auf Volumen-Leckrate

In der Vakuumtechnik wir die Leckrate allgemein als Volumen-Leckrate angegeben. Es gibt aber Berufszweige, wo die Leckrate als Gewichts-Leckrate gemessen wird. Das folgende Beispiel zeigt die Umrechnung von Gewichts- in Volumenleckrate (bei gleich bleibendem Druck und gleich bleibender Temperatur), wobei auch noch die Änderung der Gasart zwischen Betriebsgas und Suchgas berücksichtigt wird.

Deutlich wird der Unterschied in der Leckrate bei molekularer Strömung an einem Beispiel aus der Kühlgeräteindustrie. Nehmen wir an, ein Kühlschrankhersteller fordert als Qualitätsmerkmal von seinen Geräten eine Dichtheit von maximal 0,01 Gramm Frigenverlust (R-12) pro Jahr (in diesem Industriezweig ist es üblich, die Leckrate als Gewichtsleckrate anzugeben). Die entsprechende Volumen-Leckrate ist (die Umrechnung erfolgt über das mol - die molare Masse von R-12 ist 121):

121g R-12 entsprechen 22,414 Liter Gasvolumen (bei 1013 mbar und 0°C), dann sind 0,01g

$0,01 \textup{g R-12} = \frac{22,414 l \cdot 0,01 g \cdot 1 bar}{121 \textupg} = 1,85 \cdot 10^{-3} \, bar \cdot l = 1,85 \, mbar \cdot l$

Das ist die Gasmenge R-12 pro Jahr. Als Leckrate ergibt dies (das Jahr hat 3,1536 x 10⁷ Sekunden):

$q_{R-12} = \frac{1,85 mbar \cdot l}{3,1536 \cdot 10^7 s} = 5,86 \cdot 10^{-8} \, {mbar \cdot l \over s}$

Das ist aber noch nicht ganz richtig, denn das Mol ist definiert bei 0°C und 1.013 bar; der Test fand aber bei Raumtemperatur (20 Grad Celsius) statt. Wir müssen also noch entsprechend dem Gesetz von Charles, die Temperatur korrigieren:

$q_{R-12} = \frac{1,85 mbar \cdot l \cdot 293 K}{3,1536 \cdot 10^7 \, s \cdot K} = 6,3 \cdot 10^{-8} \, {mbar \cdot l \over s}$

Bei molekularer Strömung, bei gleich bleibendem Differenzdruck und gleich bleibender Temperatur ergibt sich daraus die folgende Helium-Leckrate:

$\textup{Helium-Leckrate qA} = \, ?$

$\textup{R-12 Leckrate qB} = \, 6,3 \times 10^{-8}\, {mbar \cdot l \over s}$

$\textup{molare Masse Helium} = \, 4 \, {g \over mol}$

$\textup{molare Masse R-12} = \, 121 \, {g \over mol}$

$q_A = \frac{q_B \cdot \sqrt{M_B}}{\sqrt{M_A}} = \frac{6,3 \cdot 10^{-8} {mbar \cdot l \over s}\cdot \sqrt{121 \, {g \over mol}}}{\sqrt{4 \, {g \over mol}}} = 3,5 \cdot 10^{-7} {mbar \cdot l \over s}$

Das letztgenannte Beispiel ist allerdings nicht sehr praxisnah. Es sollte nur zeigen, dass in diesem Fall die Helium- Leckrate um den Faktor von rund 5,5 größer ist als die Kühlmittel-Leckrate. In der Praxis werden Dichtheiten gefordert die zwischen 1 Gramm bis 5 Gramm Kühlmittelverlust pro Jahr liegen. Damit gelangen die Leckraten schon wieder in den laminaren Strömungsbereich.

Umrechnung von Helium-Leckrate bei molekularer Strömung auf andere Gase

Umrechnen auf:

q von Argon

q von Neon

q von Wasserstoff

q von Stickstoff

q von Luft

q von Wasserdampf

Multipliziere Helium:

0,316

0,446

1,41

0,374

0,469

Tabelle 12

Die geometrischen Abmessungen des Lecks, obwohl meistens unbekannt, haben bei molekularer Strömung im Unterschied zur laminaren Strömung unterschiedlichen Einfluss auf die Leckrate. Der Durchmesser des Lecks geht mit der dritten Potenz in die Leckrate ein (im Vergleich zur 4.Potenz bei laminarer Strömung). Bei Änderung der Gasart ändert sich die Leckrate reziprok proportional zum Quotienten der Quadratwurzeln der relativen Molekülmassen (molaren Massen).

Die Strömung im Übergangsbereich

Der Übergang von laminarer zu molekularer Strömung geschieht allmählich. Beide Strömungsarten sind vorhanden, wobei erst die eine und dann die andere Strömungsart überwiegt. Man kann dies so verstehen, dass beide Strömungsarten gemischt vorkommen, oder dass am Eintritt des Gases in die Leckkapillare laminare Strömung herrscht, die dann zum Austritt aus der Leckkapillare in molekulare Strömung übergeht.

Die mathematische Beschreibung dieses Zustandes ist schwierig. Es gibt mehrere Formeln, die diesen Zustand beschreiben, alle unterliegen gewissen Einschränkungen. Die einfachste Formel stammt von Burrow. Er hat die Formeln für laminare und molekulare Strömung miteinander kombiniert:

$q = \frac{\pi \cdot r^4}{16 \cdot \eta \cdot \textup l}\left({p_1}^2-{p_2}^2 \right) + \frac{\sqrt{2 \pi}}{6} \; \sqrt{\frac{\textup R \cdot \textup T}{M}} \frac{d^3}{l} \left(p_1 - p_2 \right)$

$q = \textup{Leckrate} = Pa \cdot m^3/s$

$\eta = \textup{dynamische Viskosität des Gases} = Pa \cdot s$

$p_1 = \textup{der höhere Druck} = Pa$

$p_2 = \textup{der niedrigere Druck} = Pa$

$R = \textup{allgemeine Gaskonstante} = 8,314 J/Mol \cdot K$

$\small \textup{dabei ist 1 Joule} = 1 Nm = 1 Ws$

$T = \textup{absolute Temperatur} = K$

$M = \textup{relative Molmasse} = He = 4$

$d = \textup{Durchmesser des Lecks} = m$

$l = \textup{Länge des Lecks} = m$

Diese Formel ist für Überschlagsrechnungen geeignet, wenn man für die geometrischen Abmessungen die Maße einer idealisierten, fiktiven Leckkapillare (runder Querschnitt, Länge größer als Durchmesser) einsetzt. Dabei schätzt man, ob die laminare oder molekulare Strömung überwiegt und benutzt die Formel von Poisseuille oder Knudsen, um die Abmessungen des fiktiven Lecks zu errechnen.

Die Ansprechzeit

Die auf Datenblättern und Spezifikationen von Lecksuchgeräten angegebenen Ansprechzeiten sind nur die Eigen -Ansprechzeiten dieser Geräte (d.h. Gerät mit angeschlossenem Referenzleck). Die Ansprechzeit einer Lecktest -Anordnung ergibt sich aus dem evakuierten Volumen des Prüfobjektes und dem effektiven Saugvermögen der angeschlossenen Pumpen. Der Quotient aus Volumen und Saugvermögen ergibt die Ansprechzeitkonstante:

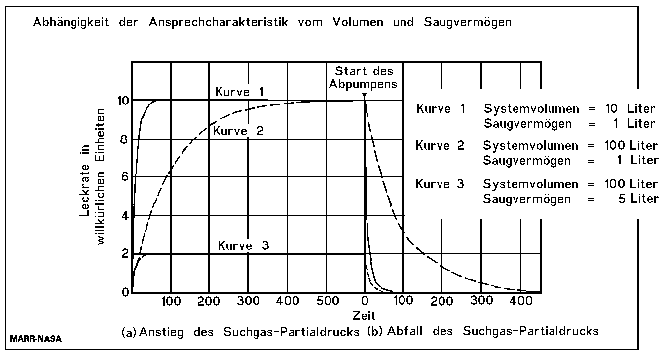
$\tau = \frac{V \, \textup{[Liter]}}{S \, \textup{[Liter/Sek]}}= \, [s]$

Beispiel: Integraler Dichtheitstest an einem Wärmetauscher

(Ein Beispiel über die Wichtigkeit der Beachtung der Ansprechzeit)

Wärmetauscher

Volumen Mantelraum:

Volumen Rohrraum:

Gesamtsaugvermögen:

3.750 l

3.176 l

17 l/s

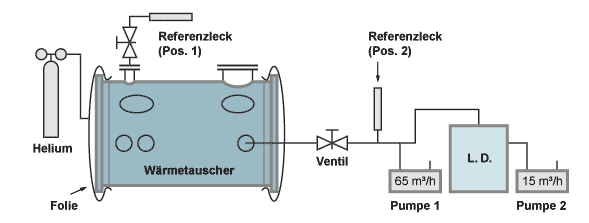Bei dem Gesamt-Saugvermögen ist der Verlust an Saugvermögen durch Strömungswiderstände berücksichtigt. Der Mantelraum wird zum Test evakiert und in den Rohrraum wird Helium eingefüllt.

Die Ansprechzeitkonstante beträgt hier:

$\tau = \frac{3760 \, l}{17 \, l/s} = 220,6 sec = 3 \, min \, 40,6 \, sec$

Zum Anstieg des Leckratensignals auf den endgültigen Wert werden ca. 5 Zeitkonstanten benötigt (siehe die folgende Tabelle), also muss, nachdem unter den Folien der Rohrraum mit 100% Helium gefüllt wurde, rund 18 Minuten und 23 Sekunden gewartet werden, bis das Messergebnis abgelesen wird.

Die Größe des Leckratensignals nach x Zeitkonstanten in %

63,2

86,46

95,02

98,16

99,3

99,75

Tabelle 13

Ansprechzeiten wie in diesem Beispiel (rund 18 Minuten) sind bei einem Integraltest überhaupt nicht hinderlich. Eine Leckortung mit einer solchen Ansprechzeit ist aber nicht möglich. Zur Leckortung muss die Ansprechzeit im Sekundenbereich liegen.