Herzlich willkommen auf den Seiten der Lecksuchtechnik

Was ist Druck?

Druck wird definiert als Kraft pro Flächeneinheit. Wie aber entsteht diese Kraft, z.B. in einem Behälter, der mit Gas gefüllt ist?
Gas besteht aus kleinen Partikeln (Molekülen und Atomen). Diese Partikel sind in dauernder Bewegung. Wenn sie irgendwo auftreffen, so üben sie dort eine Kraft aus. Wenn man eine Flächeneinheit nimmt und die Anzahl und Intensität dieser Stöße misst, so ist das eine Druckmessung.

Was ist Vakuum ?

Vakuum wird erzeugt, indem man Luft (bzw. Gas) aus einem Behälter entfernt. Es bleiben aber immer noch Partikel übrig, die ständig auf die Wandung des Behälters treffen. Es herrscht also immer noch ein Druck. Das absolute Vakuum, das praktisch nicht erreichbar ist, hätte dann den Druck "Null". Der Druck, bezogen auf das absolute Vakuum, wird Absolutdruck genannt.

Auch im Vakuum herrscht also ein Druck, wenn er auch sehr klein ist. Einen "Unterdruck" in diesem Sinne gibt es also nicht. Der Atmosphärendruck ist damit rund ein bar absolut. Manometer, die bei Atmosphärendruck Null bar anzeigen, sind "relativ" messende Instrumente. Sie zeigen den Druck relativ zum Atmosphärendruck an. Als Vakuum wird allgemein ein Druck bezeichnet, der niedriger ist als der Atmosphärendruck.

Zusammensetzung der Luft

Die Luft ist ein Gemisch von verschiedenen Gasen. Über 99 % der Luft besteht aus Stickstoff und Sauerstoff.

Der Rest sind andere Gase.

Gasart

Stickstoff

Sauerstoff

Argon

Kohlendioxid

Neon

Helium

Krypton

Wasserstoff

Xenon

Prozentsatz

78,09%

20,95%

0,93%

~0,03%

0,0018%

0,0005%

0,000114%

0,00005%

0,0000087%

Tabelle 1

Was ist Partialdruck?

Mit Partialdruck bezeichnet man den Druck, den eine einzelne Gasart in einem Gasgemisch hat. Aus der Tabelle 1 kann man die prozentuale Zusammensetzung der Luft erkennen. Bei einem Druck von 1 bar (1000 mbar) und einem Sauerstoffgehalt von 20,95 % ist dann der Partialdruck des Sauerstoffs in der Luft = 0,2095 bar oder 209,5 mbar. So kann man die Zusammensetzung des Mischgases Luft auch in folgender Tabelle mit dem Partialdruck der einzelnen Gase sehen:

Gasart

Stickstoff

Sauerstoff

Argon

Kohlendioxid

Neon

Helium

Krypton

Wasserstoff

Xenon

Partialdruck in mbar

780,9

209,5

9,3

~3 x 10^-1

1,8 x 10^-2

5 x 10^-3

1,14 x 10^-3

5 x 10^-4

8,7 x 10^-5

Tabelle 2

Daltons Gesetz

Daltons Gesetz erklärt die Zusammenhänge bei dem Partialdruck in Mischgasen

Die Summe aller Partialdrücke eines Gasgemisches ergibt dessen Totaldruck

$p_{total}=p_1+p_2+p_3+{_\dots}+p_n$

Dabei sollte man sich noch merken:

Ein Gasgemisch in einem geschlossenem Behälter entmischt sich nicht mehr, da die thermische Bewegung der Teilchen eine ständig neue Mischung erzeugt. Es ist also nicht so, daß bei einem Helium-Luft-Gemisch das Helium wegen des kleineren relativen Atomgewichts, sich wieder entmischt und nach oben steigt.

Was ist Gas ?

Gas ist Materie, bei der sich die Moleküle frei bewegen können. Diese Moleküle verteilen sich stets gleichmäßig im Raum, so dass überall der gleiche Druck herrscht. Bei Gasgemischen ist auch an jedem Ort des Raumes die Zusammensetzung des Gemisches die Gleiche. Es herrscht überall der gleiche Partialdruck.

Bei einem festen Stoff sind die Teilchen fixiert. Sie können nur vibrieren und rotieren. Bei einer Flüssigkeit sind die Teilchen weniger stark gebunden. Sie können aneinander gleiten, aber sich nicht voneinander lösen.

Was ist Dampf ?

Wenn eine Flüssigkeit oder ein fester Körper gasförmig wird, so nennen wir diesen Vorgang "verdampfen" bzw. "sublimieren".
Dieser Dampf kann wieder in die flüssige oder feste Phase zurückkehren.

Diesen Vorgang nennen wir "kondensieren" bzw. "resublimieren". Alle Dämpfe haben einen Sättigungsdampfdruck. Wenn der Druck in einem System höher wird als der Sättigungsdampfdruck, so kondensiert der Dampf. Umgekehrt gilt, solange noch eine Flüssigkeit in einem System vorhanden ist, kann man den Druck durch pumpen nicht unter den Sättigungsdampfdruck erniedrigen, weil ständig Flüssigkeit verdampft.

In einem Behälter, der eine Flüssigkeit und deren Dampf enthält und der Druck gleich dem Sättigungsdampfdruck ist, kann ständig Dampf kondensieren und Flüssigkeit verdampfen. Wasser und dessen Dampfdruck verdient in der Vakuumtechnik unsere besondere Beachtung, denn als Luftfeuchtigkeit kommt Wasserdampf in relativ großen Mengen vor. Wasser ist aus Vakuumsystemen recht schwierig zu entfernen.

Wir bezeichnen Dämpfe als die Gase, die bei normalen Temperaturen verdampfen oder kondensieren. Grundsätzlich können alle Gase kondensieren, es kommt nur darauf an, wie tief man sie kühlt.

Dampfdruck des Wassers bei verschiedenen Temperaturen

Temp in C

100

-40

-78,5

-196

Druck in mbar

1010,8

130,3

22,6

7,3

0,13

7,7 x 10^-3

1,3 x 10^-24

Tabelle 3

Dampfdruck von verschiedenen Flüssigkeiten bei 20° Celsius

Flüssigkeit

Methylalkohol

Äthylalkohol

Azeton

Wasser

Tetrachlorkohlenstoff

Hochvakuum-Diffusionspumpenöl

Druck in mbar

127,7

58,3

245,8

23,37

121,0

10^-7 bis 10^-9

Tabelle 4

Was ist freie Weglänge?

Mit mittlerer freier Weglänge bezeichnet man die Distanz, die ein Gas- oder Dampfmolekül im Durchschnitt zurücklegt, bevor es mit einem anderen Gas- oder Dampfmolekül zusammenstößt. Im Hochvakuum (bei molekularer Strömung) werden diese Distanzen so groß, dass die Gasmoleküle nur noch mit der Wandung des Gefäßes kollidieren.

Druck

Teilchen pro cm³

MFP

1013 mbar (atm)

3 x 10¹⁹30 Trillionen

6,8 x 10^-5 mm

1 x 10^-3 mbar

3 x 10¹³
30 Billionen

6,8 cm

1 x 10^-9 mbar

3 x 10⁷
30 Millionen

6,8 km

Tabelle 5

Die mittlere, freie Weglänge ist druckabhängig. Die Teilchen, die bei Atmosphärendruck alle 10tausendstel mm zusammenprallen, treffen im Mittel bei einem Druck von 10 mbar nur alle 68 km aufeinander. Die folgende Formel zeigt die mittlere, freie Weglänge für Luft bei 20 C.

$\textup{mittlere\,freie\,Wegl\"ange} = {6,8 \cdot 10^{-3}\,mbar \cdot cm \over p_{mbar}}$

Die mittlere, freie Weglänge verschiedener Gase bei 20 Grad Celsius und verschiedenen Drücken

Druck (in Pa)

Druck (in mbar)

mittlere Länge

Luft

Argon

CO₂

Wasserstoff

Wasser

Helium

Stickstoff

Neon

Sauerstoff

10^-6

10^-8

6,8

7,2

4,5

12,5

4,2

19,6

6,7

14,0

7,2

10^-3

10^-5

6,8

7,2

4,5

12,5

4,2

19,6

6,7

14,0

7,2

10^-2

6,8

7,2

4,5

12,5

4,2

19,6

6,7

14,0

7,2

10³

μm

6,8

7,2

4,5

12,5

4,2

19,6

6,7

14,0

7,2

10⁵

1000

125

196

140

Avogadro's Gesetz

Bei gleichem Druck, gleicher Temperatur und gleichem Volumen haben alle Gase die gleiche Anzahl von Teilchen.

Was ist ein Mol?

Das mol ist ein Maß für die Stoffmenge.

Warum nimmt man gerade für 1 mol das Volumen von 22,415 Litern, um die Anzahl der Gasteilchen zu bestimmen ?

Weil dann das Gewicht des Gases gleich seiner relativen Atom- oder Molekülmasse ist.
Beispiel: 1 mol Helium = 22,415 Liter wiegen (bei 0°C und 1,013 bar) 4 Gramm.

Das Gas in einem mol (22,415 Liter) hat bei 0°C und 1,013 bar (760 Torr) 6.023²³ Teilchen

Bleiben wir beim Beispiel Helium:

In einem Kubikzentimeter befinden sich dann (wieder bei NTP d.h. bei Normdruck = 1,013 bar und bei Normtemperatur von 0°C):

${6,023 \cdot 10^{23} Teilchen \over 22 \, 415 \, cm^{3}} = 2,69 \cdot 10^{19} \, {\textup{Teilchen} \over cm^{3}}$

Beispiel: Wenn man ein Vakuum mit einem Druck von 10 mbar erzeugt, also 100 mal kleiner als 1 bar, so sind in diesem Vakuum pro Kubikzentimeter immer noch 2,69 x 10¹⁹ Teilchen, d.h.:

2,69 Billionen Teilchen

Mengengrößen

Es gibt verschiedene Mengengrößen, wie in der folgenden Tabelle gezeigt:

Das Volumen [V]

Die Masse [M]

Die Teilchenzahl [N]

Die Stoffmenge [n]

falls es sich um Gas handelt:der p x V - Wert [p x V]

m³, 1, cm³

kg, g

mol, kmol

Pa * m³, mbar * l

Die relative Molekülmasse

Früher bezeichnete man diese Verhältnisse als "Atomgewicht" bzw. als "Molekulargewicht". Diese Bezeichnungen sind irreführend, weil es sich nicht um Gewichte, sondern um Verhältniszahlen handelt. Die relative Molekülmasse M (auch Molmasse oder molare Masse genannt) in SI-Einheiten ist definiert in kg/kmol. In Formeln eingesetzt ist dann die relative Molekülmasse von Helium:

M = 4 kg / kmol oder M = 4 g / mol

Boyle's Gesetz

Wenn man das Volumen eines Gases verkleinert (z.B. durch einen Kolben zusammenpresst), so erhöht sich der Druck in gleichem Maße, wenn die Temperatur dabei konstant bleibt. Halbiert man das Volumen, so verdoppelt sich der Druck.

$p1\cdot V1=p2\cdot V2$

auch bekannt als:

$p \cdot V = \textup {konstant}$

Wenn man Vakuum erzeugt, also den Druck sehr stark erniedrigt, dann expandieren Gase zu enormen Volumen (entsprechend Boyle's Gesetz). Dies geschieht auch mit absorbiertem Gas, z.B. aus Fingerabdrücken oder Schmutz.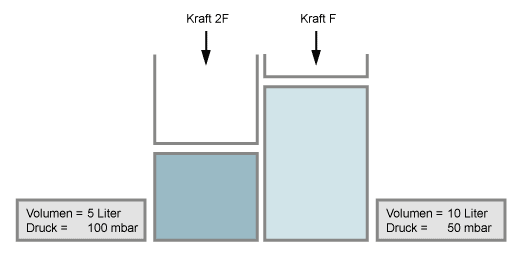

bei gleicher Anzahl von Molekülen (Temperatur konstant gehalten)

Charles Gesetz

Das Volumen eines Gases verändert sich mit der Temperatur. Wird das Gas kälter, verringert es sein Volumen; wird es wärmer, so dehnt es sich aus.

$\frac{V_1}{T_1} = \frac{V_2}{T_2}$

Wenn sich die Temperatur verdoppelt, so verdoppelt sich auch das Volumen, vorausgesetzt der Druck bleibt konstant.

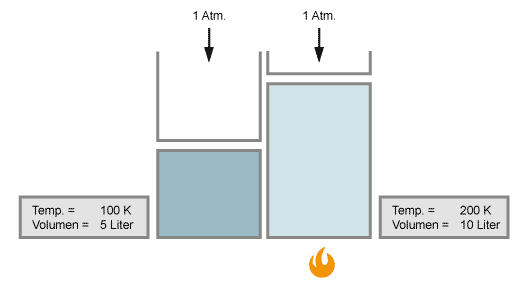
Untersucht man Charles' Gesetz noch genauer, so gelangt man zu einer noch genaueren Beziehung zwischen Gasvolumen und Temperatur, dem Gesetz von Gay-Lussac:

Das Gesetz von Gay-Lussac

Wenn die Temperatur eines Gases sich von 0 Grad Celsius um 1 Grad nach oben oder unten verändert, so vergrößert oder vermindert sich sein Volumen um 1/273stel seines ursprünglichen Wertes.

$V = V_0 \left(1+ \frac{\left \Delta T}{273k} \right)$

Lord Kelvin gelangte über dieses Gesetz zu seiner Skala für die absolute Temperatur.

Zusammenfassung:

Boyles Gesetz

beschreibt also den Zusammenhang zwischen Volumen und Druck, wobei die Temperatur und die Masse (Anzahl der Teilchen) konstant gehalten werden muss.

Charles Gesetz

beschreibt den Zusammenhang zwischen Volumen und Temperatur, wobei der Druck und die Masse konstant bleiben müssen.

Avogadro's Gesetz

beschreibt den Zusammenhang zwischen Volumen und Masse, wobei die Temperatur und der Druck konstant bleiben müssen.

Fasst man nun diese drei Gesetze zusammen, so gelangt man zum allgemeinen Gasgesetz:

Das allgemeine Gasgesetz

$p \cdot V = \nu \cdot R \cdot T$

ν(Ny) ist das Einheitszeichen für die Stoffmenge in mol bzw. kmol

Das allgemeine Gasgesetz unterliegt keiner Einschränkung, wie die Gesetze von Charles, Boyle und Avogadro.

Die Temperaturen in Charles' Gesetz und im allgemeinen Gasgesetz werden in Kelvin eingesetzt.

p =

V =

T =

ν =

R =

Druck

Volumen

Temperatur

Mol

allgemeine Gaskonstante

N/m²= Pa

m³

mol

(siehe unten)

1 bar = 10⁵Pa

Die allgemeine Gaskonstante

$R = \frac{p \cdot V}{\nu \cdot T}= 8,314 J/(\textup{mol} \cdot \textup K)$

1 J (Joule) = 1 Nm = 1 Ws

Für Berechnungen werden häufig zweckmäßig die folgenden äquivalenten Werte benutzt:

$R = 83,14 \, mbar \cdot l / mol \cdot K$

$R = 8,314 \cdot 10^{4} \, mbar \cdot l / kmol \cdot K$

$R = 8,314 \cdot 10^{3} \, Pa\:m^3 / kmol \cdot K$

Individuelle Gaskonstanten

Teilt man die allgemeine Gaskonstante durch die relative Molekülmasse (molare Masse) des entsprechenden Gases, so erhält man die individuelle Gaskonstante Ri:

$Ri = \frac{R}{M} = \frac{p \cdot V}{\nu \cdot M \cdot T} = [J/kg \cdot K]$

Gas

Luft

Argon

Helium

Wasserstoff

Stickstoff

Sauerstoff

Wasserdampf

R - 12

R - 22

287

208

2079

4116

297

260

461

68,7

96,1

Tabelle 6

Wenn man Berechnungen mit einem bestimmten Gas durchführen will, so benutzt man das allgemeine Gasgesetz mit der individuellen Gaskonstanten Ri.

$p \cdot V = \nu \cdot Ri \cdot T$

Das griechische Alphabet

Α α

Β β

Γ γ

Δ δ

Η η

Ζ ζ

Η η

Θ θ

Ι ι

Κ κ

Λ λ

Μ μ

Alpha

Beta

Gamma

Delta

Eta

Zeta

Eta

Theta

Jota

Kappa

Lambda

Ν ν

Ξξ

Ο ο

Π π

Ρ ρ

Σ σ

Τ τ

Υ υ

Φ φ

Χ χ

Ψ ψ

Ω ω

Ksi

Omikron

Rho

Sigma

Tau

Ypsilon

Phi

Chi

Psi

Omega

Die viskose Strömung

Gasmoleküle verhalten sich bei Drücken oberhalb von ungefähr 0,01 mbar ähnlich wie Flüssigkeiten. Die Moleküle sind so eng beieinander, dass sie ständig gegeneinander stoßen. Werden sie gepumpt oder herrscht eine Druckdifferenz, so strömen sie gemeinsam.

Bei der viskosen Gasströmung unterscheiden wir zwei Arten:

a.) Die turbulente Strömung, und

b.) die laminare Strömung.

Zur Abschätzung, welche Strömungsart in einem Leck zu erwarten ist, kann die folgende Tabelle dienen:

Strömungsart

turbulent

laminar

Übergangsströmung

molekular

Leckrate (mbar · l/s)

〉 10^-2

10^-1 - 10^-6

10^-4 - 10-7

〈 10^-7

Tabelle 9
Quelle: Leakage Testing Handbook, Prepared for Liquid Propulsion Section, Jet Propulsion Laboratory, National Aeronautics and Space Administration, Pasadena, California)

In der Lecksuchtechnik ist man meistens auf das Abschätzen der Strömungsart angewiesen. Es gibt natürlich Formeln zur Berechnung des Leitwertes für verschieden geformte Rohre etc. Alle diese Formeln enthalten Geometriefaktoren (Länge, Durchmesser etc.). Da bei Leckagen die Geometrie des Lecks in den meisten Fällen unbekannt ist, nützen die erwähnten Formeln nicht.

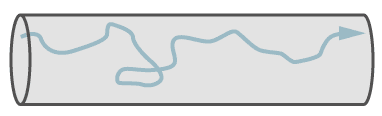
Die turbulente Strömung

Die turbulente Strömung ist eine verwirbelte Strömung. Sie tritt nur bei größeren Lecks auf und eher bei höheren Drucken. Ebenfalls ist eine hohe Geschwindigkeit des Gasstromes erforderlich. Nur Lecks mit turbulenter Gasströmung "pfeifen" und können deshalb per Schall oder Ultraschall geortet werden.

Die Formel für die Leckrate bei turbulenter Strömung wird hier nicht extra aufgeführt. Lecks mit turbulenter Strömung sind ohnehin zu groß. Sie müssen geortet und beseitigt werden und werden nur selten einer Berechnung unterzogen.

Die laminare Strömung

Die laminare Strömung wird definiert als parallele Strömung in einem Rohr, wobei die Verteilung der Geschwindigkeit der Moleküle parabolisch ist.

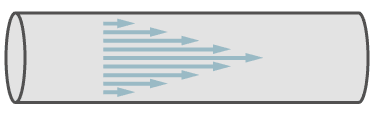
In der gezeigten Abbildung symbolisieren die Länge der Pfeile die Geschwindigkeit der Moleküle. Die bekannteste Formel für die laminare Gasströmung stammt von Poisseuille. Sie beschreibt die laminare Strömung durch ein grades Rohr mit rundem Querschnitt:

Die folgend gezeigte Formel von Poisseuille zeigt den Zusammenhang der Komponenten für die Leckrate bei laminarer Strömung.

$q = \frac{\pi \cdot r^4}{16 \cdot \eta \cdot l} \, ({p_1}^2 - {p_2}^2)$

$\eta = \textup {dynamische Viskosität des Gases}$

$l = \textup {Länge des runden Rohres (Kapillare)}$

$r = \textup {Radius der Kapillare}$

$p_1 = \textup {der h\"ohere Druck}$

$p_2 = \textup {der niedrigere Druck}$

Wenn man annimmt, dass die geometrischen Abmessungen eines Lecks, die ja meistens unbekannt sind, sich während des Zeitraums einer oder mehrerer Messungen nicht ändert, so kann man die Konstanten und die Geometriefaktoren zu einem Faktor K zusammenfassen:

$q = K \, \frac {({p_1}^2-{p_2}^2)}{\eta}$

Wobei K aus den folgenden Konstanten besteht:

$K = \, \frac {\pi \cdot r^4}{16 \cdot l}$

Wenn sich bei gleichbleibender Gasart der Differenzdruck über einem Leck ändert, so ändert sich die Leckagerate quadratisch zum Druck nach der folgenden Formel:

$\frac{q_A}{({p_{A1}}^2-{p_{A2}}^2)} = \frac{q_B}{({p_{B1}}^2-{p_{B2}}^2)}$

Man kann also durch Erhöhen der Druckdifferenz bei einer Dichtheitsprüfung die Leckrate quadratisch zum Druck erhöhen und damit eine starke Empfindlichkeitssteigerung erreichen. Bei großen Behältern, die z.B. für einen Schnüffeltest mit einem Spürgas gefüllt werden müssen, kann man eventuell Kosten sparen, indem man den Druck erhöht, aber mit einem geringeren Prozentsatz des Spürgases arbeitet. Natürlich müssen dabei die drucktechnischen Sicherheitsvorschriften beachtet werden.

Beispielberechnung

Ein interessantes Beispiel sei hier einmal berechnet, nämlich der Unterschied in der Leckrate beim Schnüffeltest und beim Vakuumtest. Die Leckgeometrie und die Gasart bleiben unverändert, ebenfalls ist der Differenzdruck über dem Leck beide Male 1 bar. Der Unterschied besteht nur darin, dass beim Vakuumtest 1 bar gegen Null bar und beim Schnüffeltest 2 bar gegen 1 bar (absolut) herrschen.

Vakuumtest

$q_A = 5 \cdot 10^{-5} \, {\textup{mbar l} \over s }$

$p_{A1} = 1 \, bar$

$p_{A2} = 0 \, bar$

Schnüffeltest

$q_{B} = \, ?$

$p_{B1} = 2 \, bar$

$p_{B2} = 1 \, bar$

Die Leckrate ist beim Schnüffeltest also drei mal größer als beim Vakuumtest, obwohl dem ersten Anschein nach der gleiche Differenzdruck vorhanden ist.

Wenn sich die Gasart ändert, so ändert sich die Leckrate umgekehrt proportional zur Viskosität der Gase.

Viskosität einiger bekannter Gase

Gasart

Luft

Stickstoff

Sauerstoff

Argon

Helium

R-12

R-22

R-134a

R-600a

Formel

N₂

O₂

CCl₂F₂

CHClF₂

CH₂F-CF₃

CH(CH₃)₂-CH₃

Viskosität bei 15°C
in Pa·s

18,0 · 10^-6

16,3 · 10^-6

19,9 · 10^-6

22,0 · 10^-6

19,2 · 10^-6

11,6 · 10^-6

12,0 · 10^-6

11,61 · 10^-6

7,4 · 10^-6

Tabelle 10

Umrechnung von Helium-Leckrate bei laminarer Strömung auf andere Gase

Umrechnen auf:

q von Argon

q von Neon

q von Wasserstoff

q von Stickstoff

q von Luft

q von Wasserdampf

Multipliziere Heliumleckrate mit:

0,883

0,626

2,23

1,12

1,08

2,09

Tabelle 11

Wie man aus dieser Tabelle erkennen kann, ist bei laminarer Strömung der Unterschied in der Leckrate zwischen den Gasen Helium und Luft nur 8 %, kleiner also als die Messgenauigkeit von Heliumlecksuchgeräten. Deshalb ist es erlaubt, wohlbemerkt bei laminarer Strömung, wenn mit einem Luft-Heliumgemisch gesucht wird, die Luft- Leckrate gleich der Helium-Leckrate zu setzen. Wenn man mit einem Helium-Luftgemisch mit 10 % Heliumgehalt arbeitet, so darf man sagen, die angezeigte Leckrate ist 10 % von der Gesamt-Leckrate.

Molekulare Strömung

Molekulare Strömung herrscht bei kleinen Leckagen (siehe Tabelle 9) und bei niedrigen Drücken. Bei molekularer Strömung wandert jedes Molekül unabhängig von anderen Molekülen. Die mittlere freie Weglänge ist größer als der Durchmesser der Leckkapillare. Damit ist es möglich, dass ein einzelnes Molekül auch gegen das Druckgefälle und die allgemeine Strömungsrichtung wandert, da sich ja die Moleküle nicht berühren, sondern nur mit den Wandungen zusammenstoßen. Trotz dieser Möglichkeit des Gegenströmens erfolgt der Gesamtfluss in Richtung des Druckgefälles. Bei molekularer Strömung fließen die Moleküle in Richtung des Partialdruckgefälles.

Die Formel von Knudsen für die Leckrate bei molekularer Strömung lautet:

$q=\frac {\sqrt{2\pi}}{ 6 } \sqrt { \frac { R\cdot T }{ M } } \frac { { d }^{ 3 } }{ l } \left( { p }_{ 1 }-{ p }_{ 2 } \right)$

$\textup {R = allgemeine Gaskonstante}$

$\textup {T = absolute Temperatur(K)}$

$\textup {M = relative Molekülmasse (molare Masse)}$

$\textup {p1 = der h\"ohere Druck}$

$\textup {p2 = der niedrigere Druck}$

$\textup {d = Durchmesser der Leckage}$

$\textup {l = Länge der Leckage}$

Aus der Formel von Knudsen kann man erkennen, dass, im Gegensatz zur laminaren Strömung, bei der molekularen Strömung sich die Leckrate in Abhängigkeit vom Druck linear proportional verändert. Zur Umrechnung der Leckrate bei verändertem Differenzdruck gilt also:

$\frac{q_A}{(P_{A1} - P_{A2})} = \frac{q_B}{(P_{B1} - P_{B2})}$

Die Abhängigkeit der Leckrate bei Änderung der Gasart folgt bei molekularer Strömung reziprok proportional der Quadratwurzel aus der relativen Molekülmasse (molare Masse). Im Gegensatz zur laminaren Strömung kann es hier größere Unterschiede in der Leckrate geben. Die Umrechnung erfolgt (bei gleichbleibendem Differenzdruck) wie in der nächsten Formel gezeigt:

$\frac{q_A}{q_B} = \frac{\sqrt{M_B}}{\sqrt{M_A}}$

Für die Umrechnung von Helium-Leckrate in Luft-Leckrate ergibt sich zum Beispiel:

$\textup {Heliumleckrate} \, q_A = 1 \cdot 10^{-8} \, {mbar \cdot l \over s}$

$\textup {relative Molek\"ulmasse Helium} = \, 4 \, {g \over mol}$

$\textup {relative Molek\"ulmasse Luft} = \, 29 \, {g \over mol}$

$\textup {Luft-Leckrate} \, q_B = \, ?$

$q_B = \frac{q_A \cdot \sqrt{M_A}}{\sqrt{M_B}} = \frac{1 \cdot 10^{-8} \, {mbar \cdot l \over s} \cdot \sqrt{4 \, {g \over mol}}}{\sqrt{29{g \over mol}}} = 3,7 \cdot 10^{-9} \, {mbar \cdot l \over s}$

Die Luftleckrate ist also bei molekularer Strömung rund 2,7 mal kleiner als die Heliumleckrate. Auf Datenblättern von Heliumlecksuchgeräten findet man noch oft, neben der Angabe der kleinsten, nachweisbaren Helium- Leckrate, die Angabe der dazu äquivalenten Luft-Leckrate, die dann um den Faktor 2,7 kleiner ist. Dies kann zu Irrtümern führen, da dieser Umrechnungsfaktor nur für die molekulare Strömung und nicht für den gesamten Messbereich des Lecksuchgerätes gilt. Helium-Lecksuchgeräte der heutigen Generation können auch millionenfach größere Leckraten messen.

Umrechnung von Gewichts-Leckrate auf Volumen-Leckrate

In der Vakuumtechnik wir die Leckrate allgemein als Volumen-Leckrate angegeben. Es gibt aber Berufszweige, wo die Leckrate als Gewichts-Leckrate gemessen wird. Das folgende Beispiel zeigt die Umrechnung von Gewichts- in Volumenleckrate (bei gleich bleibendem Druck und gleich bleibender Temperatur), wobei auch noch die Änderung der Gasart zwischen Betriebsgas und Suchgas berücksichtigt wird.

Deutlich wird der Unterschied in der Leckrate bei molekularer Strömung an einem Beispiel aus der Kühlgeräteindustrie. Nehmen wir an, ein Kühlschrankhersteller fordert als Qualitätsmerkmal von seinen Geräten eine Dichtheit von maximal 0,01 Gramm Frigenverlust (R-12) pro Jahr (in diesem Industriezweig ist es üblich, die Leckrate als Gewichtsleckrate anzugeben). Die entsprechende Volumen-Leckrate ist (die Umrechnung erfolgt über das mol - die molare Masse von R-12 ist 121):

121g R-12 entsprechen 22,414 Liter Gasvolumen (bei 1013 mbar und 0°C), dann sind 0,01g

$0,01 \textup{g R-12} = \frac{22,414 l \cdot 0,01 g \cdot 1 bar}{121 \textupg} = 1,85 \cdot 10^{-3} \, bar \cdot l = 1,85 \, mbar \cdot l$

Das ist die Gasmenge R-12 pro Jahr. Als Leckrate ergibt dies (das Jahr hat 3,1536 x 10⁷ Sekunden):

$q_{R-12} = \frac{1,85 mbar \cdot l}{3,1536 \cdot 10^7 s} = 5,86 \cdot 10^{-8} \, {mbar \cdot l \over s}$

Das ist aber noch nicht ganz richtig, denn das Mol ist definiert bei 0°C und 1.013 bar; der Test fand aber bei Raumtemperatur (20 Grad Celsius) statt. Wir müssen also noch entsprechend dem Gesetz von Charles, die Temperatur korrigieren:

$q_{R-12} = \frac{1,85 mbar \cdot l \cdot 293 K}{3,1536 \cdot 10^7 \, s \cdot K} = 6,3 \cdot 10^{-8} \, {mbar \cdot l \over s}$

Bei molekularer Strömung, bei gleich bleibendem Differenzdruck und gleich bleibender Temperatur ergibt sich daraus die folgende Helium-Leckrate:

$\textup{Helium-Leckrate qA} = \, ?$

$\textup{R-12 Leckrate qB} = \, 6,3 \times 10^{-8}\, {mbar \cdot l \over s}$

$\textup{molare Masse Helium} = \, 4 \, {g \over mol}$

$\textup{molare Masse R-12} = \, 121 \, {g \over mol}$

$q_A = \frac{q_B \cdot \sqrt{M_B}}{\sqrt{M_A}} = \frac{6,3 \cdot 10^{-8} {mbar \cdot l \over s}\cdot \sqrt{121 \, {g \over mol}}}{\sqrt{4 \, {g \over mol}}} = 3,5 \cdot 10^{-7} {mbar \cdot l \over s}$

Das letztgenannte Beispiel ist allerdings nicht sehr praxisnah. Es sollte nur zeigen, dass in diesem Fall die Helium- Leckrate um den Faktor von rund 5,5 größer ist als die Kühlmittel-Leckrate. In der Praxis werden Dichtheiten gefordert die zwischen 1 Gramm bis 5 Gramm Kühlmittelverlust pro Jahr liegen. Damit gelangen die Leckraten schon wieder in den laminaren Strömungsbereich.

Umrechnung von Helium-Leckrate bei molekularer Strömung auf andere Gase

Umrechnen auf:

q von Argon

q von Neon

q von Wasserstoff

q von Stickstoff

q von Luft

q von Wasserdampf

Multipliziere Helium:

0,316

0,446

1,41

0,374

0,469

Tabelle 12

Die geometrischen Abmessungen des Lecks, obwohl meistens unbekannt, haben bei molekularer Strömung im Unterschied zur laminaren Strömung unterschiedlichen Einfluss auf die Leckrate. Der Durchmesser des Lecks geht mit der dritten Potenz in die Leckrate ein (im Vergleich zur 4.Potenz bei laminarer Strömung). Bei Änderung der Gasart ändert sich die Leckrate reziprok proportional zum Quotienten der Quadratwurzeln der relativen Molekülmassen (molaren Massen).

Die Strömung im Übergangsbereich

Der Übergang von laminarer zu molekularer Strömung geschieht allmählich. Beide Strömungsarten sind vorhanden, wobei erst die eine und dann die andere Strömungsart überwiegt. Man kann dies so verstehen, dass beide Strömungsarten gemischt vorkommen, oder dass am Eintritt des Gases in die Leckkapillare laminare Strömung herrscht, die dann zum Austritt aus der Leckkapillare in molekulare Strömung übergeht.

Die mathematische Beschreibung dieses Zustandes ist schwierig. Es gibt mehrere Formeln, die diesen Zustand beschreiben, alle unterliegen gewissen Einschränkungen. Die einfachste Formel stammt von Burrow. Er hat die Formeln für laminare und molekulare Strömung miteinander kombiniert:

$q = \frac{\pi \cdot r^4}{16 \cdot \eta \cdot \textup l}\left({p_1}^2-{p_2}^2 \right) + \frac{\sqrt{2 \pi}}{6} \; \sqrt{\frac{\textup R \cdot \textup T}{M}} \frac{d^3}{l} \left(p_1 - p_2 \right)$

$q = \textup{Leckrate} = Pa \cdot m^3/s$

$\eta = \textup{dynamische Viskosität des Gases} = Pa \cdot s$

$p_1 = \textup{der höhere Druck} = Pa$

$p_2 = \textup{der niedrigere Druck} = Pa$

$R = \textup{allgemeine Gaskonstante} = 8,314 J/Mol \cdot K$

$\small \textup{dabei ist 1 Joule} = 1 Nm = 1 Ws$

$T = \textup{absolute Temperatur} = K$

$M = \textup{relative Molmasse} = He = 4$

$d = \textup{Durchmesser des Lecks} = m$

$l = \textup{Länge des Lecks} = m$

Diese Formel ist für Überschlagsrechnungen geeignet, wenn man für die geometrischen Abmessungen die Maße einer idealisierten, fiktiven Leckkapillare (runder Querschnitt, Länge größer als Durchmesser) einsetzt. Dabei schätzt man, ob die laminare oder molekulare Strömung überwiegt und benutzt die Formel von Poisseuille oder Knudsen, um die Abmessungen des fiktiven Lecks zu errechnen.

Die Ansprechzeit

Die auf Datenblättern und Spezifikationen von Lecksuchgeräten angegebenen Ansprechzeiten sind nur die Eigen -Ansprechzeiten dieser Geräte (d.h. Gerät mit angeschlossenem Referenzleck). Die Ansprechzeit einer Lecktest -Anordnung ergibt sich aus dem evakuierten Volumen des Prüfobjektes und dem effektiven Saugvermögen der angeschlossenen Pumpen. Der Quotient aus Volumen und Saugvermögen ergibt die Ansprechzeitkonstante:

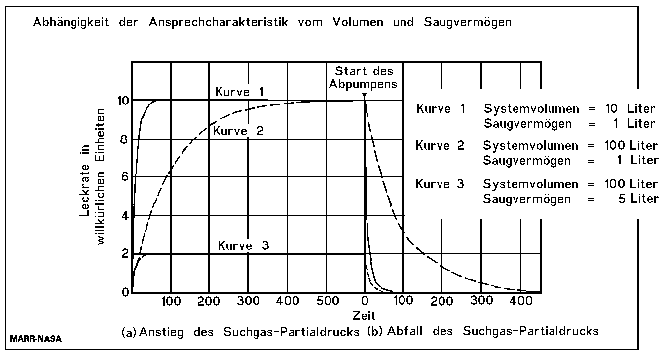
$\tau = \frac{V \, \textup{[Liter]}}{S \, \textup{[Liter/Sek]}}= \, [s]$

Beispiel: Integraler Dichtheitstest an einem Wärmetauscher

(Ein Beispiel über die Wichtigkeit der Beachtung der Ansprechzeit)

Wärmetauscher

Volumen Mantelraum:

Volumen Rohrraum:

Gesamtsaugvermögen:

3.750 l

3.176 l

17 l/s

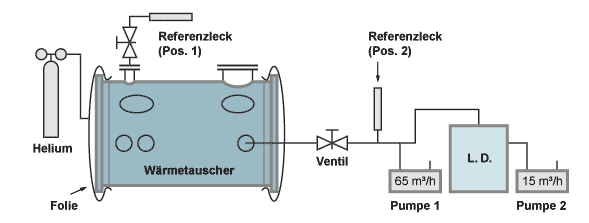Bei dem Gesamt-Saugvermögen ist der Verlust an Saugvermögen durch Strömungswiderstände berücksichtigt. Der Mantelraum wird zum Test evakiert und in den Rohrraum wird Helium eingefüllt.

Die Ansprechzeitkonstante beträgt hier:

$\tau = \frac{3760 \, l}{17 \, l/s} = 220,6 sec = 3 \, min \, 40,6 \, sec$

Zum Anstieg des Leckratensignals auf den endgültigen Wert werden ca. 5 Zeitkonstanten benötigt (siehe die folgende Tabelle), also muss, nachdem unter den Folien der Rohrraum mit 100% Helium gefüllt wurde, rund 18 Minuten und 23 Sekunden gewartet werden, bis das Messergebnis abgelesen wird.

Die Größe des Leckratensignals nach x Zeitkonstanten in %

63,2

86,46

95,02

98,16

99,3

99,75

Tabelle 13

Ansprechzeiten wie in diesem Beispiel (rund 18 Minuten) sind bei einem Integraltest überhaupt nicht hinderlich. Eine Leckortung mit einer solchen Ansprechzeit ist aber nicht möglich. Zur Leckortung muss die Ansprechzeit im Sekundenbereich liegen.

Helium-Massenspektrometer-Lecktest an druckbeaufschlagten (gebombten) hermetisch geschlossenen Bauteilen

Übersetzung einer Veröffentlichung der Fa. Varian über den Helium-Bombing- Test

Beim Drucklagerungstest, dem sogenannten "Bombing-Test" werden kleine, schon hermetisch geschlossene Bauteile auf Dichtheit geprüft, indem sie in einem Druckbehälter (der sogenannten Bombe) mit dem Spürgas unter Druck eine gewisse Zeit lang beaufschlagt werden. In ein undichtes Bauteil wird das Spürgas (z.B. Helium) eindringen und kann dann unter einer Glocke am Lecksuchgerät evakuiert werden. Dabei wird das eingedrungene Helium wieder heraustreten und als Leckrate angezeigt werden

Der Zusammenhang zwischen angezeigter und wahrer Leckrate

Die beim Dichtheitstest von hermetisch geschlossenen "gebombten" Bauteilen, wie z.B. Transistoren, Dioden und integrierten Schaltkreisen, am meisten gestellte Frage ist die nach dem Zusammenhang zwischen der abgelesenen und der wahren Leckrate.

Die Antwort, die abhängt ist von Faktoren wie internes Volumen des Bauteils, der Bombingzeit und der Wartezeit, liegen die Leckraten im allgemeinen relativ nahe beieinander, innerhalb einer Größenordnung, bei den meisten so geprüften Bauteilen.

Um diesen Zusammenhang aufzuzeigen, haben wir die folgenden Formel von den Gasgesetzen abgeleitet. Diese Formel gilt für alle nicht kondensierbaren Gase.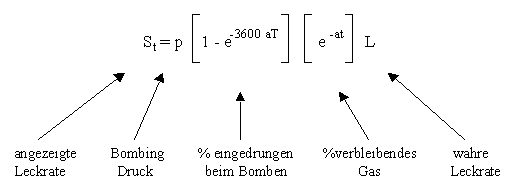

$S_t = \textup {angezeigte Leckrate} \: (mbar \cdot l/s)$

$p = \textup {Bombingdruck} \: (bar \, abs)$

$T = \textup {Bombingzeit} \: (\textup {Stunden})$

$t = \textup {Wartezeit} \: (\textup {Sekunden})$

$L = \textup {wahre Leckrate} \: (mbar \cdot l/s)^*$

$a = L/V \: (V = \textup {internes Volumen in} \, cm^3)$

* die Leckrate, welche gemessen würde, wenn das Bauteil 100% Spürgas bei Atmosphärendruck enthielte.

Das Resultat sind 14 Seiten mit 3.360 tabularisch erfassten angezeigten Leckraten über einen weiten Bereich von Volumen und Zeiten etc. Jede Seite repräsentiert einen Wert der wahren Leckrate L. Alle Werte sind kalkuliert für einen Bombingdruck von einem bar (die Luft aus der Bombe entfernt und mit 1 bar absolut Spürgas ersetzt). Multiplizieren Sie den Bombingdruck in bar abs. um den korrekten Wert von St zu erhalten. Da die vorhandene Leckrate linear proportional zum Druck ansteigt (molekulare Strömung), sind die erhaltenen Werte von St konservativ korrekt.

Ein hermetisch geschlossenes Bauteil mit einem internen Volumen von 10³ mm³ (10^-2 cm³) wird in einen Druckbehälter platziert. Dieser wird zuerst evakuiert (oder mit Helium gespült) und dann auf einen Druck von 4 bar (5 bar absolut) gebracht und so über 3 Stunden gehalten. Danach wird das Teil entnommen und unter einer kleinen Glocke am Lecksuchgerät evakuiert und die Leckrate gemessen. Der Test findet 5 Minuten nach der Entnahme des Bauteils aus dem Druckbehälter (der Bombe) statt. Angenommen das Bauteil hat ein Leck von 1 x 10^-6 mbar·l/s, die zu erwartende Größe der abgelesenen Leckrate kann wie folgt gefunden werden:

Zuerst suchen Sie die Kolonne mit der Überschrift "BOMB TIME 3 HOURS". Dann suchen Sie horizontal das Volumen von 10^-2 cm³ und dort die Wartezeit (WAIT TIME) von 300 sec. (5 Minuten). Sie finden die Leckrate St = 6,41 x 10^-7 mbar·l/s (Std cc/ sec [Standard cm/Sekunde] kann man gleich setzen mit mbar.l/s)*. Da der Bombingdruck 5 bar abs. betrug, multiplizieren Sie diese Leckrate mit 5 und erhalten als zu erwartende abzulesende Leckrate 3,2 x 10^-6mbar·l/s. Umgekehrt kann die am Lecksuchgerät abgelesene Leckrate durch den Druck p dividiert und dieser Wert in der entsprechenden Kolonne aufgesucht werden (wenn T, t und V bekannt sind). Die gefundene wahre Leckrate ergibt einen konservativen Wert (d.h. gleich oder größer als die wahre Leckrate).

Um das Interpretieren der Tabellen noch besser zu erläutern, haben wir Beispiele für ein großes und ein kleines Volumen und ein großes und kleines Leck ausgewählt und diese in vier möglichen Kombinationen aus den Tabellen ausgewählt (bei einem Bombingdruck von 5 bar abs.). Damit erhalten wir ein Grobleck, zwei kleine Lecks und ein nicht mehr nachweisbares Leck.

* In der Übersetzung wurden die alten, in dem Original von 1968 benutzten und im englischen Sprachgebrauch üblichen Bezeichnungen für Leckrate und Druck (Std.cc/s und Atm etc.) durch die heute gültigen SI-Einheiten ( mbar·l/s und bar etc.) ersetzt. Auf den Kopien der Tabellen stehen noch die alten Bezeichnungen. Genau betrachtet ist ein Standard-Kubikzentimeter Gas ein Kubikzentimeter bei Normaldruck (1013 mbar) und Normaltemperatur (0°C), umgerechnet in mbar.l also 1,013 mbar·l. In der Praxis der Lecksuchtechnik kann man den kleinen Unterschied vernachlässigen und vereinfachend sagen Std·cc/s = mbar l/s.

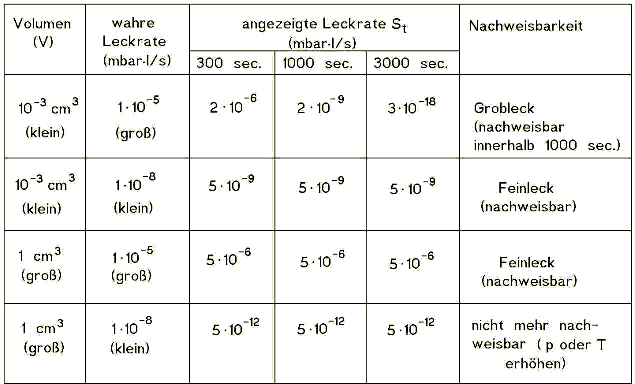
Das Grobleck kann innerhalb von 17 Minuten noch gemessen werden (1000 Sekunden). Das nicht mehr nachweisbare Leck kann gemessen werden, indem man die Bombingzeit und/oder den Bombingdruck vergrößert. Hiermit wird erkenntlich, dass mit Hilfe der Tabellen die Bedingungen ermittelt werden können, innerhalb welcher Sie die Leckraten Ihres Produktes messen können.

Auf den nächsten Bildern sind diese Beispiele grafisch dargestellt. Beim Beispiel 1 ist das interne Volumen bereits nach einer Stunde gefüllt. Eine Verlängerung der Bombingzeit hat damit keinen Einfluss auf das schließlich zu messende Signal. Wenn dieses Bauteil aus der Bombe genommen wird, so entweicht das Spürgas schnell. Die Kurve kreuzenden Striche zeigen, dass die Anzeige der nominellen Leckrate schon in weniger als 200 Sekunden erreicht wird und 50% dessen sind schon nach 250 Sekunden erreicht.

Bei den anderen drei Beispielen ist der Anstieg der Gasfüllung fast linear, da die Füllung des internen Volumens von 5 bar (oder 500% Helium) nicht erreicht wird. Im Beispiel 2 und 3 wird nur ein Zehntel der Füllung (oder 50% von 1 bar abs.) erreicht. Da die Gasverlustrate nach Herausnehmen des Bauteils aus der Bombe sehr klein ist, ist es möglich, noch 2 - 3 Stunden nach der Entnahme zu testen, ohne eine wesentliche Verkleinerung der angezeigten Leckrate. In diesem Falle ist die angezeigte Leckrate ungefähr 50% von der wahren Leckrate.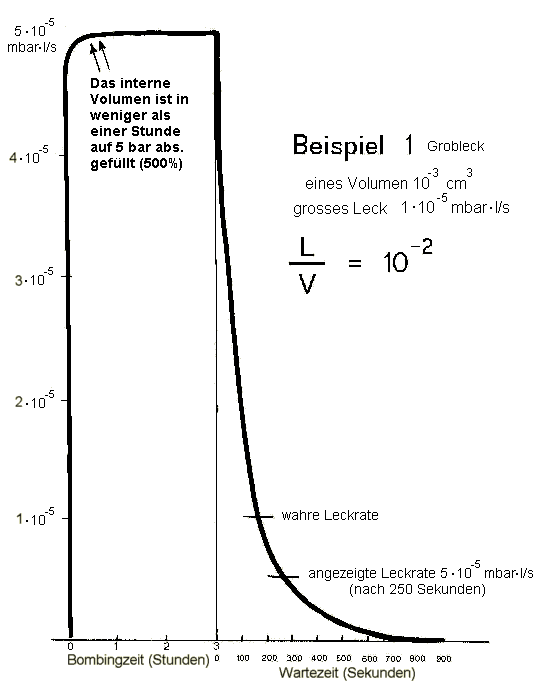

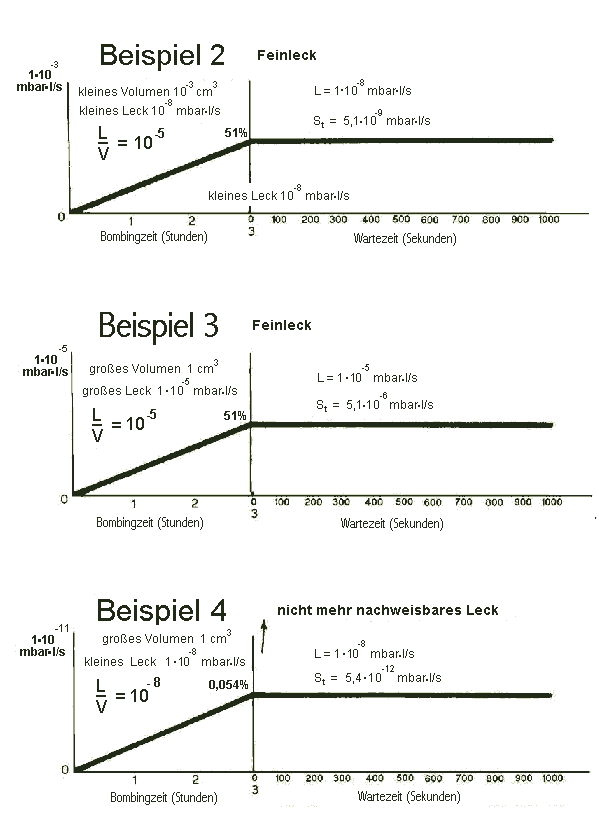
Im Beispiel 4 ist die Form der Kurve praktische die gleiche, aber der Prozentsatz der Heliumfüllung ist extrem klein, ca. eintausend mal kleiner als in den anderen beiden Beispielen. Eine Erhöhung der Bombingzeit und/oder des Bombingdrucks kann das zu messende Signal in den Nachweisbereich des Lecksuchgerätes bringen.

Wenn man diese Kurven näher betrachtet, erkennt man, dass das Verhältnis der wahren Leckrate zum internen Volumen (L/V) ein wichtiger Parameter zur Bestimmung der Art des Einfließen und Ausfließen des Spürgases bei gegebener Bombing- und Wartezeit ist. In den Beispielen 2 und 3 ist das L/V-Verhältnis das Gleiche. Damit ist auch die prozentuale Füllung des internen Volumens mit dem Spürgas das gleiche, nämlich 51%. Damit ist die abgelesene Leckrate auch 51% von der wahren Leckrate L.

In der nächsten Abbildung ist eine Kurvenschar aufgetragen, die den Füllgrad in % gegen das Verhältnis L/V zeigt, und zwar bei einem Bombingdruck von 5 bar (abs.), einer Bombingzeit von 3 Stunden und Wartezeiten von 300, 1000 und 10 000 Sekunden. Für andere Bombingzeiten können gleichermaßen Kurven gezeichnet werden. Die Prozente des Füllgrades, hier bezeichnet mit dem Faktor K, entsprechen der doppelten Klammer der Exponentialfunktion in der obigen Formel hier noch multipliziert mit dem Faktor 5, um den Bombingdruck von 5 bar einzubringen. Der maximale Füllgrad ist in diesem Falle 500% bzw. 5 bar.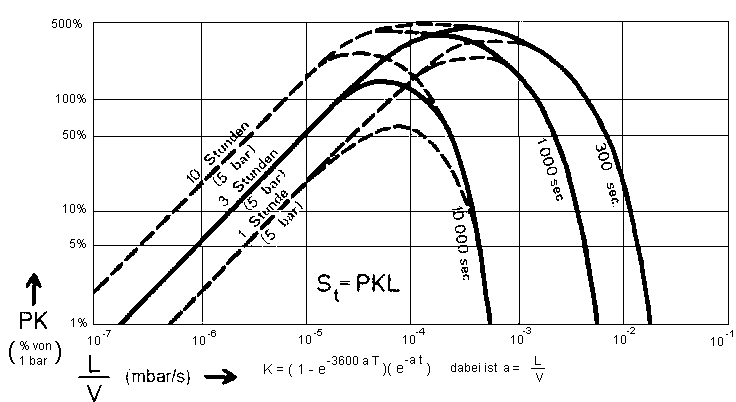

Die Anwendung dieser Kurven kann gut am Beispiel 2 illustriert werden. Das Verhältnis L/V ist dort 10^-5 mbar/sec

$\frac{L}{V} = \frac{10^{-8} mbar \cdot l}{s \cdot 1000 \cdot 10^{-6}l} = 10^{-5} mbar/s$

Wenn man nun die L/V-Teilungslinie von 10^-5 nach oben verfolgt, so schneidet sie die Kurve (Beispiel 2 - Bombingzeit 3 Std.) bei 51%. Damit ist die angezeigte Leckrate 51% von 1 x 10^-8 nämlich 5,1 x 10^-9 mbar l/s. Man beachte, dass dies unabhängig von der Wartezeit ist, zumindest bis 10.00 Sekunden.

Dieser Prozentsatz würde auch für jedes andere Testobjekt gelten, geprüft unter diesen Bedingungen, vorausgesetzt es hat ein L/V-Verhältnis von 10^-5 mbar/s . Zum Beispiel trifft es auch zu für ein Prüfobjekt mit dem internen Volumen von 10² cm³und einer Leckrate von 1 x 10^-7 mbar l/s. Hier wäre die angezeigte Leckrate 51% von 1 x 10^-7, nämlich 5,1 x 10^-8 mbar·l/s.

Dies gilt also auch für das Beispiel 3 mit L = 10^-5 mbar l/s und V = 1 cm^-3. Wieder ist hier das Verhältnis L/V = 10^-5 mbar/s und damit der Füllgrad 51% und auch die angezeigte Leckrate 51% von 10^-5 mbar l/s = 5,1 x 10^-6mbar l/s.

Noch interessanter ist das Beispiel 1. Hier ist die Leckrate 1 x 10^-5 mbar l/s und das Volumen 10^-3 cm³. Damit ist L/V = 10² mbar/s. Nach einer Wartezeit von 300 Sekunden ist die Spürgasfüllung auf rund 20% abgefallen und damit die angezeigte Leckrate 20% von 1 x 10^-5 = 2 x 10^-6 mbar l/s - wenn der Test 300 Sekunden nach der Entnahme durchgeführt wird. Der Verlust an Spürgas geschieht hier sehr schnell. Nicht erkennbar in dieser Darstellung ist, dass dennoch nach einer Wartezeit von 1000 Sekunden (17 Minuten) die 10^-5sec^-1-Linie noch 0,02% aufweist und damit eine Leckrate von 2 x 10^-9 angezeigt wird.

Um zu zeigen, wie eng der Zusammenhang zwischen St und L ist, zeigt der folgende Auszug aus den Tabellen. Dieser Auszug umfasst zwei Volumina, 10^-3 und 10^-2 cm³ (womit die meisten hermetisch geschlossenen, elektronischen Bauteile erfasst sind), und die wahren Leckraten von 10^-5 bis 10^-7 mbar l/s. Starke Anhaltspunkte zeigen, dass buchstäblich alle Lecks (L) an Glas-zu-Metall-, Keramik-zu-Metall-Verbindungen etc. Leckraten von 5 x 10^-7 Std·cm³/s oder größer haben. Die Zahlen dieser Tabelle sind ein Auszug aus der 14-seitigen Originaltabelle, wobei der Bombingdruck auf 5 bar festgelegt wurde. Auch ist diese Tabelle zum schnelleren Ablesen neu geordnet.

Es ist bedeutsam, dass die Werte der angezeigten Leckraten innerhalb einer halben Größenordnung zur wahren Leckrate liegen, für alle Werte außer denen der ersten Kolonne. Dort ist es notwendig, innerhalb einer Wartezeit von 300 bis 1000 Sekunden zu testen, um Ergebnisse zu erhalten, die vernünftig nahe zur wahren Leckrate liegen. Damit liefert diese Tabelle einen guten Überblick, warum die Resultate der Dichtheitsmessungen mit der Bombing- Technik an geschlossenen Bauteilen sinnvolle Aussagen ermöglichen

W.E. Briggs
S.G Burnett
Oktober 1968

Einleitung

Es folgen nun die Beschreibungen der am häufigsten angewandten Lecksuch- und Dichtheits-Messverfahren, ohne einen Anspruch auf Vollständigkeit zu erheben. Die Zahl der mögliche Verfahren ist beliebig groß. Um hier ein exotisches Verfahren zu nennen: Man nehme ein Schmetterlingsweibchen und sperre es in einen Behälter, bei dem eine Leckage vermutet wird. Außen läßt man ein Schmetterlingsmännchen fliegen. Ein Schmetterlingsmännchen kann ein Weibchen schon aus 2 Kilometer Entfernung wittern. So wird also das Schmetterlingemännchen sich genau auf der Leckagestelle niederlassen.

Der Blasentest

Der Blasentest ist wohl die älteste Lecksuchmethode überhaupt (Schon die alten Römer...). Man fülle ein Gefäß mit Luftüberdruck und halte es unter Wasser. Bekannt ist der Lecktest mit dem Fahrradschlauch. Doch auch hier gibt es einiges zu beachten. Wenn man ein Gefäß mit hohem Gasdruck füllt, besteht die Gefahr des Berstens. So ein Bersten kann dramatische Zerstörungen verursachen. Also muss man Vorsichtsmaßnahmen treffen.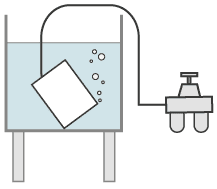

Bei höherem Fülldruck muss zwischen dem Wasserbad und dem Betrachter eine Schutzwand angebracht sein und die Blasenbildung muss über Spiegel beobachtet werden.

Nun gibt es Behälter, die zu groß sind um in eingetaucht zu werden. Hier hilft man sich, indem die kritischen Stellen des Behälters (z.B. Schweißnähte) mit einer schaumbildenden Flüssigkeit eingesprüht werden. Es gibt speziell für diesen Zweck hergestellte Flüssigkeiten in Spraydosen.

Für die Anwendung mit schaumbildenden Flüssigkeiten gibt es etliche Variationen. Wenn z.B. ein Boden eines großen Tanks mit dem Blasentest auf Dichtheit geprüft werden soll, so hat man unter dem Boden keinen Hohlraum, der mit Luft- Überdruck gefüllt werden könnte. Hier streicht man die Schweißnaht mit der schaumbildenden Flüssigkeit ein, platziert eine Vakuumglocke mit Schauglas darüber und erzeugt unter der Glocke ein Vakuum. An einer Leckstelle werden sich Blasen bilden.

Für diese Tests gilt, wie für alle visuellen Verfahren: Das menschliche Auge ist kein zuverlässiges Messinstrument. Selbst bei hoher Konzentration des Prüfenden können Fehler unterlaufen.

Die Nachweisempfindlichkeit der Blasentest-Verfahren ist schwierig zu definieren. Wenn ein Prüfer eine Fläche von ca. 10 Quadratzentimetern eine Viertelstunde lang mit der Lupe bei guter Beleuchtung betrachten kann, so kann er die Entwicklung einer Blase beobachten, die einer Leckrate von 10^-7mbar l/s entspräche. Wenn aber die Schweißnähte von 500 Rohren an einem Wärmetauscher auf Schaumbildung beobachtet werden müssen, so kann man höchsten eine Nachweisempfindlichkeit von 10^-4mbar l/s annehmen.

Druckänderungsverfahren

Dichtheitsprüfungen mittels Druckänderungsverfahren ergeben stets die Gesamtleckrate eines Prüfobjektes. Es sind sogenannte integrale Dichtheitsmessungen. Man unterscheidet die Druckabfallmessung, die Druckanstiegsmessung und die Differenzdruck-Messung.

Die Druckabfallmessung

Bei der Druckabfallmessung wird das Prüfobjekt mit einem Gas (meistens Luft) auf einen Überdruck gefüllt. Bei dem Vorhandensein einer Leckage wird der Druck mit der Zeit abfallen. Aus der Druckdifferenz multipliziert mit dem Volumen dividiert durch die Messzeit kann die Leckrate errechnet werden.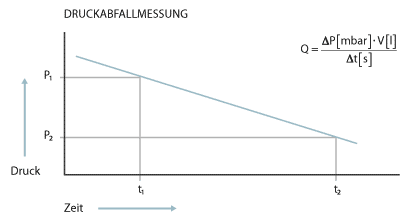

Bei der Druckabfall-Messung muss der Druck sehr präzise gemessen werden. Die Temperatur muss möglichst konstant gehalten werden. Eine Temperaturänderung um wenige Grad Celsius kann eine Druckänderung bewirken, die größer ist als der Druckabfall infolge einer Leckage.

Wenn der gasförmige Fülldruck mehrere bar Überdruck beträgt, muss vor dem Druckabfalltest ein Festigkeitstest durchgeführt werden. Dieser Test wird meistens mit einer Wasserfüllung durchgeführt mit einem 1,3-fachen des Betriebsdruckes. Die luftblasenfreie Wasserfüllung bewirkt, im Gegensatz zur Gasfüllung, keine Explosion, wenn das Prüfobjekt einen Riss bekommen sollte. Diese sogenannte Wasserdruckprobe kann auch als grober Dichtheitstest gesehen werden. Das Entweichen von geringsten Wassermengen bewirkt eine deutliche Druckänderung. Auch hier bewirkt eine Temperaturänderung eine Druckänderung, denn der Ausdehnungskoeffizient von Wasser ist größer als der von Stahl.

Generell kann man sagen, dass für kleine Volumina das Verfahren geeignet ist. Je größer das zu untersuchende Volumen wird, um so fehlerbehafteter wird die Messung.

Die Druckanstiegsmessung

Bei der Druckanstiegsmessung wird das Prüfobjekt evakuiert und der Druckanstieg über die Zeit gemessen. Der Nachteil der Druckabfallmessung, nämlich bei hohem Druck noch sehr kleine Druckdifferenzen messen zu müssen, wird bei der Druckanstiegsmessung weitgehend umgangen. Da das Prüfobjekt zu dieser Messung evakuiert wird, ist die Gasmenge zu Beginn der Messung bedeutend kleiner und die Druckänderung kann nicht größer als 1 bar werden.

Allerdings ergibt sich bei dieser Messung zuerst ein Druckanstieg in Folge der Abgasung von an der Wandung haftenden Gasen - vorwiegend Wasserdampf. Dadurch ergibt sich eine gekrümmte Druckanstiegskurve. Erst wenn der Sättigungsdampfdruck des Wassers überschritten ist, wird der Kurvenverlauf linear und erst dann kann wieder aus Volumen, Druckdifferenz und Messzeit die Leckrate ermittelt werden. Eine grafische Darstellung der Messung ist hier unerlässlich.

Die Differenzdruckmessung

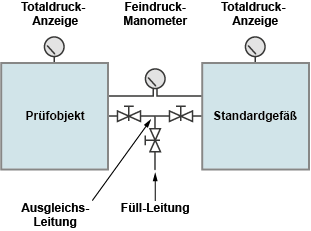Die Druckdifferenzmessung ist die genaueste Methode der Leckratenmessung unter den Druckänderungsverfahren, aber auch die komplizierteste in der Ausführung. Man füllt das Prüfobjekt mit einem hohen Druck (soweit es zulässig ist) und vergleicht diesen Druck mit dem Druck in einem Standardgefäß, dessen Dichtheit unzweifelhaft feststeht.

Beide Behälter werden langsam auf einen gleichen Druck gefüllt. Der Druck muss in beiden Behältern stets gleich sein, andernfalls könnte das empfindliche Druckdifferenz-Messgerät zerstört werden. Dann wird der Druckabfall im Prüfobjekt durch Messung der Druckdifferenz zum Standardgefäß gemessen. Dabei ist es möglich, bei einem Prüfdruck von z.B. 10 bar, ein Druckmessgerät mit einem Vollausschlag von z.B. 100 mbar und einer Anzeigegenauigkeit von 1 mbar zu benutzen.

Wie schon Eingangs erwähnt, ergeben diese Messungen keine Aussage über die örtliche Lage der Leckage. Wird also ein Leck festgestellt, muss es danach mit anderen Verfahren geortet werden, es sei denn das Prüfobjekt ist ein billiges Massenteil, das als Ausschuss weggeworfen werden kann.

Kurzfassung

Die immer mehr an Bedeutung gewinnende Dichtheitsprüfung mit dem Spürgas Helium und dem Nachweis mit einem Massenspektrometer-Helium-Lecksuchgerät wird in der praktischen Anwendung an Röhrenwärmetauschern beschrieben. Dabei werden drei unterschiedliche Testanordnungen besprochen.

Der Integraltest mit Vakuum im Mantelraum und Helium bei Atmosphärendruck im Rohrraum.

Dabei wird die Testvorbereitung, die korrekte Vorgehensweise beim Test, der Pumpvorgang und die Ansprechzeitkonstante beschrieben. Ebenfalls wird auf die verwendbaren Dichtungen und auf Problemlösungen bei negativem Testausgang eingegangen.

Der Integraltest mit Helium-Überdruck im Mantelraum und Vakuum im Rohrraum.

Dieser Test wird oft erforderlich, wenn in den Mantelraum schon einmal Helium eingefüllt war, z.B. zur Leckortung mit der Schnüffelsonde. Hier wird auf die veränderten Testbedingungen und die Berechnung der Leckrate bei Druckänderung eingegangen und es wird auf die Möglichkeit der Einsparung von Helium durch Druckerhöhung hingewiesen.

Der Integraltest mit Helium-Überdruck im Mantelraum und Atmosphärendruck im Rohrraum.

Dieser Test erfordert lange Wartezeiten. Er wird nur benutzt, wenn die anderen Methoden nicht durchführbar sind und wenn ein hoher Heliumdruck im Mantelraum angewendet werden kann. Bei diesem Test wird der Anstieg der Heliumkonzentration im Rohrraum gemessen. Die Größe der Leckagerate erhält man nur durch Berechnung. Die Durchführung dieses Tests sowie die Berechnung der Wartezeit und der Leckagerate werden beschrieben.

Eigenschaften von Spürgasen

Gas

Name

Wasserstoff

Helium

Luft

molare Masse

g/mol

2,016

4,003

28,89

Viskosität

μPa s

8,9

19,8

18,36

Thermische
Geschw.

m/s

1770

1256

467

mittlere freie
Weglänge

μm

198

126

68,5

Wärmeleit-
fähigkeit

W/m K

0,149

0,183

0,0275

Die Lecksuche mit Spürgasen (engl. Tracer Gases) sind die empfindlichsten Nachweisverfahren. Mit Helium als Spürgas kann man unter extrem sauberen Laborbedingungen noch Leckageraten im 10^-12mbar l/s Bereich nachweisen. Das entspricht einem Gasverlust von ca. 1 Kubikzentimeter in 30 000 Jahren.

Die Methode mit dem Spürgas Helium und dem Nachweis mit einem Massenspektrometer wurde in den USA um das Jahr 1945 entwickelt. Eine der ersten Veröffentlichungen stammt von Nier (1947, siehe unter Literaturangaben).

Bevor es die Helium-Lecksuche gab, war die empfindlichste Lecksuchmethode die Halogen-Lecksuche. Als Spürgas wurde R-12 (Freon bzw. Frigen) verwendet und unter besten Bedingungen war eine Leckrate von 10^-8mbar l/s nachweisbar. Diese Methode wird kaum noch angewandt, da umweltschädliche Fluor- chlorkohlenwasserstoffe als Spürgade verwendet werden. Deshalb wird hier auf die Beschreibung dieser Testmethode verzichtet. In Kälteanlagen werden heute Ersatzgase benutzt. Für Lecksuche an solchen Anlagen gibt es Massenspektrometer-Lecksuchgeräte für schwerere Gase als Helium oder Wasserstoff.

Darüber hinaus gibt es noch ein Lecksuchverfahren mit Ammoniak, bei dem das Prüfobjekt mit diesem Gas gefüllt und außen mit nassem Lackmuspapier beklebt wird. Eine Farbänderung an dem Papier zeigt die Stelle der Leckage. Das letzte erwähnte Verfahren ist das der Wärmeleitungsmessung: das Prüfobjekt wird mit dem Spürgas gefüllt wobei man ein Gas bevorzugen sollte, das sich in der Wärmeleitung von der Luft- Wärmeleitung deutlich unterscheidet. Die größten Unterschiede zur Luft haben die Gase Wasserstoff und Helium. Mit einem speziellen Schnüffelgerät, bestückt mit einem Wärmeleitungs-Sensor wird nach dem Ort der Leckage gesucht. Grundsätzlich sollte man ein Gas bevorzugen, das sich in der Wärmeleitung von der Luft- Wärmeleitung deutlich unterscheidet. Die größten Unterschiede zur Luft haben die Gase Wasserstoff und Helium.

Leckortungsverfahren

1.) Lecksuche von außen nach innen: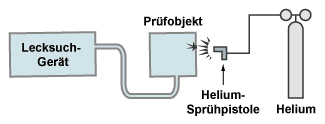

Das Prüfobjekt wird über das Lecksuchgerät evakuiert. Von außen wird es mit einem schwachen Heliumstrahl aus einer Sprühpistole abgesprüht. Gelangt Helium über eine Leckage in das Vakuum im Prüfobjekt, wird dieses vom Massenspektrometer erfasst und empfindlich angezeigt. Indem man die Sprühpistole langsam über das Prüfobjekt bewegt, findet man den Punkt mit der größten Anzeige am Lecksuchgerät.

Bei dieser Prüfmethode muss die Ansprechzeit im Sekundenbereich liegen. Je länger die Ansprechzeit, um so langsamer muss die Sprühpistole bewegt werden. Hat man die Leckage geortet und verweilt nun mit dem Sprühstrahl über der Leckage, kann die Größe der Leckage vom Lecksuchgerät angezeigt werden. Das setzt eine 100%ige Einströmung von Helium durch die Leckage und ein mit einem Referenzleck kalibrierten Lecksuchgerät voraus.

Diese Methode gestattet den empfindlichsten Nachweis, da im Vakuum des Prüfobjektes fast kein störender Helium-Untergrund vorhanden ist.

2.) Lecksuche von innen nach außen: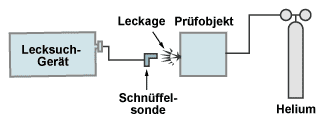

Bei dieser Leckortungsmethode wird das Prüfobjekt mit Helium gefüllt. Am Helium-Lecksuchgerät ist eine Schnüffelsonde angebracht, durch die ständig ein schwacher Luftstrom zum Lecksuchgerät gesaugt wird. Führt man die Schnüffelsonde nun am Prüfobjekt über die kritischen Bereiche und gelangt dabei Helium statt Luft in die Schnüffelsonde, so wird dies dort angezeigt.

Diese Prüfmethode ist besonders geeignet, wenn sich bei der Vakuum-Methode lange Ansprechzeiten ergeben würden. Bei der Schnüffelsonde wird die Ansprechzeit nur durch die Länge der Schnüffelleitung bestimmt. Sie liegt bei einer gängigen Schlauchlänge von 3 Metern in Bereich von einer Sekunde. Sind lange Schnüffelleitungen erforderlich, so gibt es ein Verfahren, das üblicherweise "Quick Test" genannt wird. Dabei wird der Gastrom durch die Schnüffelleitung mit einer Membranpumpe erhöht. Da aber dieser größere Gasfluss nicht insgesamt in das Lecksuchgerät geleitet werden kann, ist die Empfindlichkeit dieser Methode geringer.

Gegenüber der Vakuum-Methode ist die Schnüffelmethode bedeutend unempfindlicher, da sich in der Luft 5 ppm Helium befinden. Das entspricht einem Partialdruck von 5 x 10^-3 mbar. Dieser Heliumanteil in der Atmosphäre wird vom Helium-Lecksuchgerät deutlich als Untergrundsignal nachgewiesen und empfindlicher als das Untergrundsignal kann nicht gemessen werden. So liegt die Nachweisgrenze bei der Helium-Schnüffelmethode bei rund 2 x 10^-6 mbar l/s.

Messung der Gesamtleckrate

Die Messung der Gesamtleckrate wird auch Integraltest genannt. Sie kann wiederum auf zweierlei Art ausgeführt werden, nämlich erstens von außen nach innen und zweitens von innen nach außen. Diese Art der Messung gibt keine Auskunft über die örtliche Lage der Leckage.

1.) Integraltest von außen nach innen: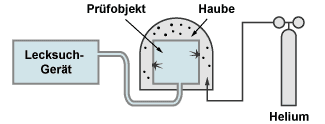

Das Prüfobjekt wird vom Helium-Lecksuchgerät evakuiert. Von außen wird es von einer Hülle oder Glocke umgeben, die mit Helium gefüllt wird. Um eine Messung der Gesamtleckrate zu erlangen, muss unter der Hülle 100% Helium sein. Bei einer Glocke kann man dies erreichen, indem man vor dem Füllen mit Helium die Glocke evakuiert. Bei einer Hülle, die das Evakuieren nicht zulässt (z.B. eine Hülle aus einer Folie) muss man die 100%ige Füllung durch Spülen erreichen. Dazu muss die Hülle auch eine Austrittsöffnung haben. Dort kann man mit einem am Lecksuchgerät über einen Schlauch angeschlossenem geeichten Kapillarleck die Heliumkonzentration messen.

Bei dieser Art der Messung spielt die Ansprechzeit keine Rolle. Die Leckanzeige steigt dann entsprechend langsam an. Man darf das Messergebniss erst ablesen, wenn sich die Leckanzeige nicht mehr ändert.

2.) Integraltest von innen nach außen: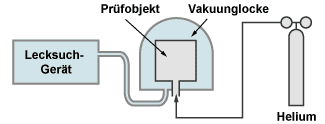

Das vollständig mit Helium gefüllte Bauteil wird unter einer Glocke angebracht, die vom Helium-Lecksuchgerät evakuiert wird. Jegliches aus der Leckage entweichende Helium gelangt so zum Lecksuchgerät und wird dort quantitativ angezeigt. Für die Ansprech-Zeitkonstante ist das Restvolumen unter der Glocke dividiert durch das effektiv wirksame Saugvermögen an der Glocke maßgebend.

Bei großen Bauteilen, die nicht mehr unter einer Glocke angebracht werden können, gibt es ein Ersatzverfahren. Man umhüllt das Prüfobjekt mit einer Folie und misst den Anstieg der Heliumkonzentration unter der Folie. Dabei muss die Wartezeit und auch die sich ergebende Leckrate errechnet werden. Bei langen Ansprechzeiten muss die Folie metallisiert sein, sonst ergeben sich Heliumverluste durch Permeation durch die Folie. Eine detaillierte Beschreibung dieses Verfahrens ist in meinem Seminar für Dichtheitsmessungen und Lecksuchmethoden zu finden.

Die Lecksuche mit Wasserstoff

Die Lecksuche mit dem Spürgas Wasserstoff spielte wegen der Gefährlichkeit des Gases bisher kaum eine Rolle. Inzwischen aber gibt es einen Halbleiter-Sensor, der Wasserstoff mit einer Empfindlichkeit von 0,5 ppm nachweisen kann. Auch der Wasserstoffgehalt der Luft ist sehr klein, nämlich auch 0,5 ppm (um den Faktor 10 kleiner als der Untergrund beim Helium). So wird es interessant, mit einem Spürgasgemisch von 5% Wasserstoff und 95% Stickstoff mit diesem Sensor Lecksuche und Dichtheitstests zu betreiben. Dieses Gemisch ist weder brennbar noch explosiv. Es ist unter dem Namen Formiergas erhältlich.

Da auch die Energieversorgung mit Wasserstoff ein zukunftsträchtiges Thema ist und bereits heute Anwendungen existieren (z.B. Brennstoffzelle, Kfz-Antrieb etc.), so gibt es auch schon Geräte und Anlagen, die mit Wasserstoff gefüllt sind oder damit betrieben werden. Dort bietet sich die Lecksuche mit diesem Sensor geradezu an. Man kann zwar auch Massenspektrometer-Lecksuchgeräte auf Wasserstoff abstimmen, aber der Halbleiter-Sensor erlaubt eine Lecksuche ohne Vakuumsystem und damit geringerem technischen Aufwand.

Der Wasserstoff-Sensor ist ein Halbleiterelement auf Metallhydrid-Basis. Er reagiert sehr empfindlich auf Wasserstoff. Dabei ändert sich sein Strom. Dies wird zur Leckagemessung genutzt. Die Lecksuche funktioniert etwas anders als die Helium-Lecksuche. Der Wasserstoff-Sensor sitzt direkt in der Schnüffelsondenspitze. Es wird kein Gas angesaugt sondern das aus einem Leck austretende Formiergas gelangt durch Diffusion an die dicht vorbeigeführte Schnüffelsonde. Es ist nur die Schnüffelmethode anwendbar. Ein Test von außen nach innen (bei evakuiertem Testobjekt) ist nicht möglich.

So gibt es mit dem Wasserstoff Lecksuchgerät nur die folgenden Testmethoden:

1.) Leckortung (von innen nach außen) durch absuchen mit der Schnüffelsonde

2.) Integraltest von innen nach außen : Das mit Formiergas gefüllte Prüfobjekt wird unter eine Haube gestellt und mit der Wasserstoff-Schnüffelsonde wird der Anstieg der Wasserstoffkonzentration gemessen.

Die Lecksuche mit Laserstrahlen

Es gibt auch Verfahren zum Nachweis von Leckagen mittels Laserstrahlen. Dabei wird ein Prüfobjekt mit einem Spürgas auf einen bestimmten Überdruck gefüllt. Von außen wird das Prüfobjekt mit einem CO2-Laserstrahl abgetastet.

Trifft der Laserstrahl auf eine Leckage, kenntlich durch das dort austretende Gas, so wird dieses Gas vom Laserstrahl zu einem höheren Energiezustand angeregt, d.h. ein oder mehrere Elektronen der Gasmoleküle werden auf eine höhere Bahn befördert. Beim Zurückfallen auf die ursprüngliche Bahn wird diese Energie wieder freigegeben. Dies äußert sich durch eine Emission von Photonen (ein Lichtblitz mit einer bestimmten Frequenz [Farbe]).

Diese Lichtblitze werden durch einen geeigneten Sensor registriert und mit dem Abtastraster des Laserstrahls synchronisiert. Auf einem Monitor erhält man dann ein Bild des Prüfobjekts, auf dem der Ort der Leckage erkennbar ist.

Die Permeation von Gasen

Unter Permeation versteht man das Durchdringen von Gasen durch einen fehlerfreien, festen Stoff.

Die Massenspektrometer-Helium Lecksuchgeräte sind noch immer das Nonplusultra in der Leck- suchtechnik, wenn es um höchste Empfindlichkeit, großen Messbereich (10 Dekaden und mehr), Vielfalt der Anwendungen, usw. geht. Aber sie benötigen ein Vakuumsystem mit mechanischer Vorvakuum- und Hochvakuumpumpe und einen Netzanschluss zur Energieversorgung. Ein Batteriebetrieb ist nicht möglich. Die Nachfrage nach solchen batterieberiebenen Helium-Lecksuchgeräten hat Entwicklungen hervorgerufen, die den Heliumnachweis mit Hilfe der Permeation dieses Gases durch Quarz-Material ausnutzen.

Die Firma Varian hat 1991 das erste batteriebetriebene, tragbare Schnüffel-Helium-Lecksuchgerät herausgebracht, das mit einem patentierten Verfahren Helium mit Hilfe der Permeation von anderen Gasen trennte. Das Gerät hieß "Helitest", gefolgt von der Weiterentwicklung "PHD-4".

Mit der Sampling-Pumpe wird über die Schnüffelsonde (Probe) Gas angesaugt und an der erhitzten Quarz-Kapillare vorbeigeblasen. Ist bei dem angesaugten Gas Helium anteilig dabei, gelangt dieses schnell durch Permeation in das Innere der Kapillare. Andere Gase permeieren nicht durch die Quarz-Kapillare. Dort herrscht ein Vakuum von ca. 10 mbar. Durch das eingedrungene Helium ändert sich der Pumpenstrom in der Mini-Ionengetterpumpe. Der Mikroprozessor rechnet das in Leckrate um, die am Display angezeigt wird.

Die Fa. Inficon folgte mit der Entwicklung von Helium-Lecksuchgeräten nach dem Permeationsprinzip und brachte 2006 das Gerät Protec 3000 auf den Markt. Wie das später angebotene T-Guard Helium-Schnüffelgerät arbeiten diese Geräte nach der Wise- Technologie™

Protec3000 T-Guard

Der Wise Technology™Sensor besteht aus einem evakuierten Glasgehäuse, welches an einer Seite von einem Siliziumwafer mit integrierter Siliziumdioxid-Membran verschlossen wird. Diese Membran ist nur 7 µm dick und wird im Betrieb auf über 200 °C erhitzt. Siliziumdioxid ist Helium-permeabel, d.h. Helium kann Siliziumdioxid durchqueren. Dieser Effekt wird auch bei Helium-Permeationslecks ausgenutzt. Durch unterschiedliche Helium- Partialdrücke auf beiden Seiten der Membran gelangt Helium in die evakuierte Glaszelle. Durch die dünne Membran und die hohe Temperatur geschieht dies besonders schnell.
In der Glaszelle werden die Heliumatome durch eine Penningentladung nachgewiesen. Bei diesem Nachweis wird das Helium durch eine hohe Beschleunigungsspannung tief in die Kathode eingeschossen und dadurch der Absolutdruck im Glasgehäuse wieder gesenkt. In diesem Sinne wird das Helium also von einer Ionen-Getter-Pumpe nachgewiesen, nachdem es durch eine Siliziumdioxid-Membran aus der Luft „gefiltert“ wurde. Die Auflösung des Wise Technology™Sensors liegt bei einem Helium-Partialdruck von ca. 10^-6mbar.

Links zu den Firmen Varian und Inficon finden Sie auf der Seite: "Links zu anderen Lecksuchadressen", wo Sie sich weitere Informationen über diese Geräte verschaffen können.

Historische Literatur Vakuumtechnik

Verfasser	Titel	erschienen bei:
Otto v. Guericke	Neue Magdeburger Versuche	VDI-Verlag, Düsseldorf 1968
H. Ebert	Vakuum-Chronik	PTB Braunschweig 1977, ISSN 9341-6682

Historische Literatur Lecksuchtechnik

Verfasser	Titel	erschienen bei:
A.J.Dempster	A New Method Of Positive Ray Analysis	Phys. Rev. 11, 316, 1918
A.O. Nier	A Mass Spectrometer for Routine Isoptope Abundance Measurements	Rev. Sci. Instr., 11,212, July 1940
Thomas, Williams, Axd, Hipple	A Mass Spectrometer Type of Leak Detector	Rev. Sci. Inst. Vol. 17, 10, 1946
A.O. Nier et al	Mass Spectrometer for Leak Detection	J.Appl.Phys. 18, 30, Jan 1947
Nier, Stevens, Hustrulid, Abbott	Mass Spectrometer for Leak Detection	J. Appl. Phys. Vol. 18. 1947
Ochert, Steckelmacher	Leak Detection Practice	Vacuum, Vol. II, No. 2, 1952
Douglass, Charpentier	A Simplified Mass Spectrometer	Net. Symp. Vac. Trans. London, 1956
Mongodin	l´Hélitest, Spectromtré de Mass Détecteur de Fuites.	Proc. 1st. Cong. Vac. Tech. Namur, 1958
H.W. Drawin, K.Kronenberger	Ein neues, universell einsetzbares Lecksuch-Massenspektrometer	Vac. Tech. 8 H 5, 1959
NN, Lab basses Press. 87 Rue A G	Helium Leckdetektor: Helitest	Zit. in Vak. Tech 12, H 7,138, 1959
Cosutta, Steckelmacher	Lens mass-spectrometer leak detector	J. Sci. Instr. Vol. 37, 1960
F. Kirchner und A. Benninghoven	Über ein doppeltfokussierendes Massenspektrometer	Vak. Tech. 12, H 7, 207, 1963
G. Reich	Massenspektrometer mit hoher Partialdruckempfindlichkeit für Lecksucher	Trans 3, Int. Vac. Cong. Stuttg. 1965
NN	L`Etancheite A Pierrelatte..("Diatron 18"),	Le Vide Nr. 108, 11 ff, ca 1965
A.H. Turnbull	Leak detection and detectors (20th Century L.D.)	Vacuum 15 / 1, 3 ff, 1965
Bültemann	Streuionenunterdrückung beim Gasdetektor	ME4, MAT, Lab.-Ber., Fr. Krupp,
W. Becker	Anordnung zur Lecksuche nach dem Massenspektrometer-Prinzip	Auslegeschrift 1648648 D.Patentamt
W. Becker	Erhöhung der Empfindlichkeit des He-Lecksuchers durch Verwendung einer Turbomolekularpumpe	Vak.-Technik 17 H 8, 1968
W. Becker, W.K. Huber et.al.	A novel helium leak detector with turbomolecular pump	Int.Vak. Congr. Vienna Sept. 1977
Chr. Falland	Experiences with helium leak detection	Int.report DESY M-79/34 Hamburg
Chr. Falland	Ein neuer einfacher Universal Lecksucher mit luftgekühlter Turbopumpe	Vakuumtechnik 29 H, 7.Okt. 1980
Chr. Falland	Dichtigkeitesprüfung und Lecksuche, Methodenübersicht u. Entwicklungen	Int. Ber. DESY M81/26 Hamburg Sept. 1981

Basis Literatur Vakuumtechnik

Verfasser	Titel	erschienen bei:
Wutz, Adam, Walcher	Theorie und Praxis der Vakuumtechnik	Vieweg, Braunschweig, 5. Aufl. ISBN 3-528-34884-4
Karl Jousten, Max Wutz	Vakuuktechnik, Theorie und Praxis	Vieweg-Verlag ISBN-10: 383480133X ISBN-13: 978-3834801333
Kerspe	Vakuumtechnik in der industriellen Praxis	expert verlag, Sindelfingen, 1987
A. Roth	Vacuum Technology	North Holland Verlag

Zeitschriften

Verfasser	Titel	erschienen bei:
Deutsche Gesellschaft für Zerstörungsfreie Prüfung	Link zur Zeitschrift: http://www.dgzfp.de/	DGZfP
	Vakuum Praxis	VCH, Weinheim
The e-Journal of Nondestructive Testing	Link zur Zeitschrift: http://www.ndt.net	expert verlag, Sindelfingen, 1987
European Federation for Non-Desturctive Testing	Link zur Zeitschrift: http://www.efndt.org	EFNDT

Basis Literatur Lecksuchtechnik

Verfasser	Titel	erschienen bei:
Editor: Master	Non Destructive Testing Handbook, Vol. 1, Leak- Detection	ASNT, ASM / USA 1982, ISBN 0-87170-125-1
General Electric	Leakage Testing Handbook	Schenectady, New York, 1996
Hal Greenhouse	Hermeticity of Electronic Packages	ISBN: 0815514352, Pub. Date: April 2000
Kernforschungszentrum Karlsruhe	Ein neuartiges Helium-Lecksuchgerät	Kernforschungszentrum Karlsruhe: ASIN
Klaus Kutzke	Dichtheitsprüfung und Lecksuche mit dem Helium-Leckdetektor	Expert-Verlag (Febr. 1998) ISBN-10: 3816908225 ISBN-13: 978-3813908227
	Leckagen (Sondereinband)	ISBN-10: 3802727010 ISBN-13: 978-3922429852
Verlag: Deutsche Kälte und Klimatechnik, Eckart Prandner	Maßnahmen zur Verhinderung von Ammoniak-Leckagen und Folgeschäden	ISBN-10: 3922429858 ISBN-13: 978-3922429852
Verlag Glückauf, Benno Ring	Vergleichende Untersuchungen zur thermischen und hydraulischen	ISBN-10: 3773913141 ISBN-13: 978-3773913142
Expert-Verlag, Gerhard Wiegleb	Industrielle Gas-Sensorik	ISBN-10: 3816919561 ISBN-13: 978-38166919568
Shaker-Verlag, Martin Hauser	Silizium-basiertes Sensorsystem zur Erfassung von Spurengasen in Luft mittels mikrostruktuierter Multielektroden	ISBN-10: 3826530853 ISBN-13: 978-3826530852
L.Hütten	Praxis der Dichtheitsprüfung mit Helium	Alcatel Selbstverlag
Varian	Introduction to Helium Mass Spectrometer Leak Detection	Lexington, Massachusets, 1995 Liberary of Congress Catalog

Europäische Normen zur Dichtheitsprüfung

Nummer	Deutscher Titel der Norm	Bemerkung
DIN EN 1330-8	Zerstörungsfreie Prüfung - Terminologie - Begriffe für die Dichtheitsprüfung	in drei Sprachen
DIN EN 1518	Zerstörungsfreie Prüfung - Dichtheitsprüfung - Charakterisierung von massenspektrometrischen Leckdetektoren	angelehnt an ISO 3550
DIN EN 1779	Zerstörungsfreie Prüfung - Dichtheitsprüfung - Kriterien zur Auswahl von Prüfmethoden und Verfahren	Harmonized Supporting
DIN EN 1593	Zerstörungsfreie Prüfung - Dichtheitsprüfung - Blasenprüfverfahren	Harmonized Supporting Standard
DIN EN 13184	Zerstörungsfreie Prüfung - Dichtheitsprüfung - Druckänderungsverfahren	Harmonized Supporting Standard
DIN EN 13185	Zerstörungsfreie Prüfung - Dichtheitsprüfung - Prüfgasverfahren	Harmonized Supporting Standard
DIN EN 13192	Zerstörungsfreie Prüfung - Dichtheitsprüfung - Kalibrierung von Referenzlecks für Gase
DIN EN 13625	Zerstörungsfreie Prüfung - Dichtheitsprüfung - Anleitung zur Wahl von Dichtheitsprüfgeräten	Supporting Standard

Weitere Normungsanträge zur Dichtheitsprüfung liegen zur Zeit nicht vor.

In Deutschland ist die Bezugsquelle der bekannte Beuth-Verlag, siehe auch DIN-Webseite:

http://www2.din.de/

Allgemeine Literatur

Hanser Fachbuchverlag, Martin Bantel	Messgeräte-Praxis. Funktionen und Einsatz moderner Messgeräte	ISBN-10: 3446217649 ISBN-13: 978-3446217645
Verlag Oldenbourg, Tilo Pfeifer	Fertigungsmesstechnik	ISBN-10: 3486257129 ISBN-13: 978-3486257120
Verlag Teubner, Manfred Busch, Gerhard Eyb, Joachim Messner, Heinz Stetter	Messtechnik an Maschinen und Anlagen	ISBN-10: 3519063263 ISBN-13: 978-3519063261
Verlag Wiley-Vch, Karl Heinz Näser, Gerhard Peschel	Physikalische Meßmethoden	ISBN-10: 3342003715 ISBN-13: 978-3342003717