Der Zusammenhang zwischen angezeigter und wahrer Leckrate

Die beim Dichtheitstest von hermetisch geschlossenen "gebombten" Bauteilen, wie z.B. Transistoren, Dioden und integrierten Schaltkreisen, am meisten gestellte Frage ist die nach dem Zusammenhang zwischen der abgelesenen und der wahren Leckrate.

Die Antwort, die abhängt ist von Faktoren wie internes Volumen des Bauteils, der Bombingzeit und der Wartezeit, liegen die Leckraten im allgemeinen relativ nahe beieinander, innerhalb einer Größenordnung, bei den meisten so geprüften Bauteilen.

Um diesen Zusammenhang aufzuzeigen, haben wir die folgenden Formel von den Gasgesetzen abgeleitet. Diese Formel gilt für alle nicht kondensierbaren Gase.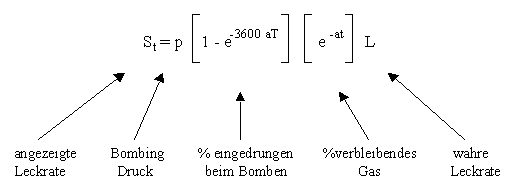

* die Leckrate, welche gemessen würde, wenn das Bauteil 100% Spürgas bei Atmosphärendruck enthielte.

Das Resultat sind 14 Seiten mit 3.360 tabularisch erfassten angezeigten Leckraten über einen weiten Bereich von Volumen und Zeiten etc. Jede Seite repräsentiert einen Wert der wahren Leckrate L. Alle Werte sind kalkuliert für einen Bombingdruck von einem bar (die Luft aus der Bombe entfernt und mit 1 bar absolut Spürgas ersetzt). Multiplizieren Sie den Bombingdruck in bar abs. um den korrekten Wert von St zu erhalten. Da die vorhandene Leckrate linear proportional zum Druck ansteigt (molekulare Strömung), sind die erhaltenen Werte von St konservativ korrekt.

Ein hermetisch geschlossenes Bauteil mit einem internen Volumen von 10³ mm³ (10^-2 cm³) wird in einen Druckbehälter platziert. Dieser wird zuerst evakuiert (oder mit Helium gespült) und dann auf einen Druck von 4 bar (5 bar absolut) gebracht und so über 3 Stunden gehalten. Danach wird das Teil entnommen und unter einer kleinen Glocke am Lecksuchgerät evakuiert und die Leckrate gemessen. Der Test findet 5 Minuten nach der Entnahme des Bauteils aus dem Druckbehälter (der Bombe) statt. Angenommen das Bauteil hat ein Leck von 1 x 10^-6 mbar·l/s, die zu erwartende Größe der abgelesenen Leckrate kann wie folgt gefunden werden:

Zuerst suchen Sie die Kolonne mit der Überschrift "BOMB TIME 3 HOURS". Dann suchen Sie horizontal das Volumen von 10^-2 cm³ und dort die Wartezeit (WAIT TIME) von 300 sec. (5 Minuten). Sie finden die Leckrate St = 6,41 x 10^-7 mbar·l/s (Std cc/ sec [Standard cm/Sekunde] kann man gleich setzen mit mbar.l/s)*. Da der Bombingdruck 5 bar abs. betrug, multiplizieren Sie diese Leckrate mit 5 und erhalten als zu erwartende abzulesende Leckrate 3,2 x 10^-6mbar·l/s. Umgekehrt kann die am Lecksuchgerät abgelesene Leckrate durch den Druck p dividiert und dieser Wert in der entsprechenden Kolonne aufgesucht werden (wenn T, t und V bekannt sind). Die gefundene wahre Leckrate ergibt einen konservativen Wert (d.h. gleich oder größer als die wahre Leckrate).

Um das Interpretieren der Tabellen noch besser zu erläutern, haben wir Beispiele für ein großes und ein kleines Volumen und ein großes und kleines Leck ausgewählt und diese in vier möglichen Kombinationen aus den Tabellen ausgewählt (bei einem Bombingdruck von 5 bar abs.). Damit erhalten wir ein Grobleck, zwei kleine Lecks und ein nicht mehr nachweisbares Leck.

* In der Übersetzung wurden die alten, in dem Original von 1968 benutzten und im englischen Sprachgebrauch üblichen Bezeichnungen für Leckrate und Druck (Std.cc/s und Atm etc.) durch die heute gültigen SI-Einheiten ( mbar·l/s und bar etc.) ersetzt. Auf den Kopien der Tabellen stehen noch die alten Bezeichnungen. Genau betrachtet ist ein Standard-Kubikzentimeter Gas ein Kubikzentimeter bei Normaldruck (1013 mbar) und Normaltemperatur (0°C), umgerechnet in mbar.l also 1,013 mbar·l. In der Praxis der Lecksuchtechnik kann man den kleinen Unterschied vernachlässigen und vereinfachend sagen Std·cc/s = mbar l/s.

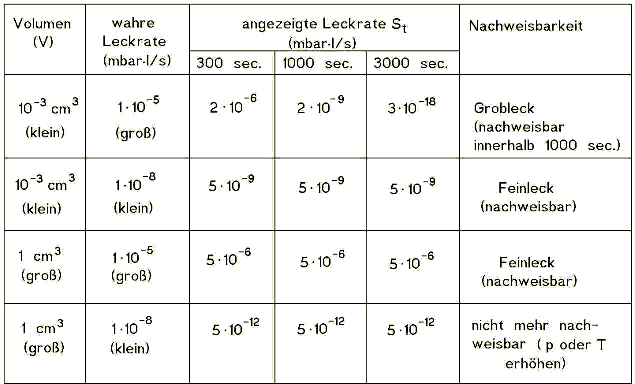
Das Grobleck kann innerhalb von 17 Minuten noch gemessen werden (1000 Sekunden). Das nicht mehr nachweisbare Leck kann gemessen werden, indem man die Bombingzeit und/oder den Bombingdruck vergrößert. Hiermit wird erkenntlich, dass mit Hilfe der Tabellen die Bedingungen ermittelt werden können, innerhalb welcher Sie die Leckraten Ihres Produktes messen können.

Auf den nächsten Bildern sind diese Beispiele grafisch dargestellt. Beim Beispiel 1 ist das interne Volumen bereits nach einer Stunde gefüllt. Eine Verlängerung der Bombingzeit hat damit keinen Einfluss auf das schließlich zu messende Signal. Wenn dieses Bauteil aus der Bombe genommen wird, so entweicht das Spürgas schnell. Die Kurve kreuzenden Striche zeigen, dass die Anzeige der nominellen Leckrate schon in weniger als 200 Sekunden erreicht wird und 50% dessen sind schon nach 250 Sekunden erreicht.

Bei den anderen drei Beispielen ist der Anstieg der Gasfüllung fast linear, da die Füllung des internen Volumens von 5 bar (oder 500% Helium) nicht erreicht wird. Im Beispiel 2 und 3 wird nur ein Zehntel der Füllung (oder 50% von 1 bar abs.) erreicht. Da die Gasverlustrate nach Herausnehmen des Bauteils aus der Bombe sehr klein ist, ist es möglich, noch 2 - 3 Stunden nach der Entnahme zu testen, ohne eine wesentliche Verkleinerung der angezeigten Leckrate. In diesem Falle ist die angezeigte Leckrate ungefähr 50% von der wahren Leckrate.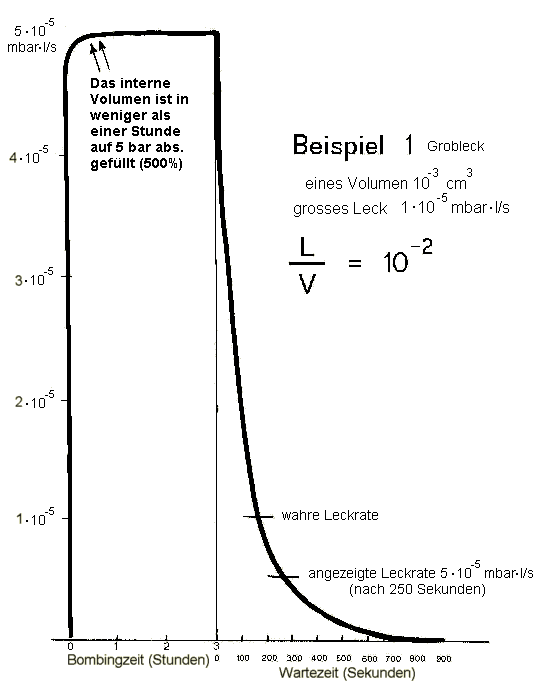

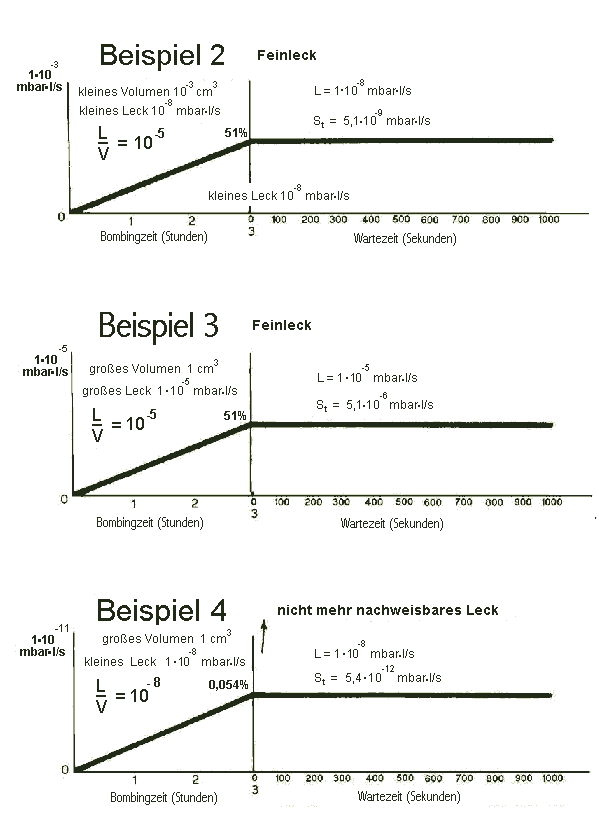
Im Beispiel 4 ist die Form der Kurve praktische die gleiche, aber der Prozentsatz der Heliumfüllung ist extrem klein, ca. eintausend mal kleiner als in den anderen beiden Beispielen. Eine Erhöhung der Bombingzeit und/oder des Bombingdrucks kann das zu messende Signal in den Nachweisbereich des Lecksuchgerätes bringen.

Wenn man diese Kurven näher betrachtet, erkennt man, dass das Verhältnis der wahren Leckrate zum internen Volumen (L/V) ein wichtiger Parameter zur Bestimmung der Art des Einfließen und Ausfließen des Spürgases bei gegebener Bombing- und Wartezeit ist. In den Beispielen 2 und 3 ist das L/V-Verhältnis das Gleiche. Damit ist auch die prozentuale Füllung des internen Volumens mit dem Spürgas das gleiche, nämlich 51%. Damit ist die abgelesene Leckrate auch 51% von der wahren Leckrate L.

In der nächsten Abbildung ist eine Kurvenschar aufgetragen, die den Füllgrad in % gegen das Verhältnis L/V zeigt, und zwar bei einem Bombingdruck von 5 bar (abs.), einer Bombingzeit von 3 Stunden und Wartezeiten von 300, 1000 und 10 000 Sekunden. Für andere Bombingzeiten können gleichermaßen Kurven gezeichnet werden. Die Prozente des Füllgrades, hier bezeichnet mit dem Faktor K, entsprechen der doppelten Klammer der Exponentialfunktion in der obigen Formel hier noch multipliziert mit dem Faktor 5, um den Bombingdruck von 5 bar einzubringen. Der maximale Füllgrad ist in diesem Falle 500% bzw. 5 bar.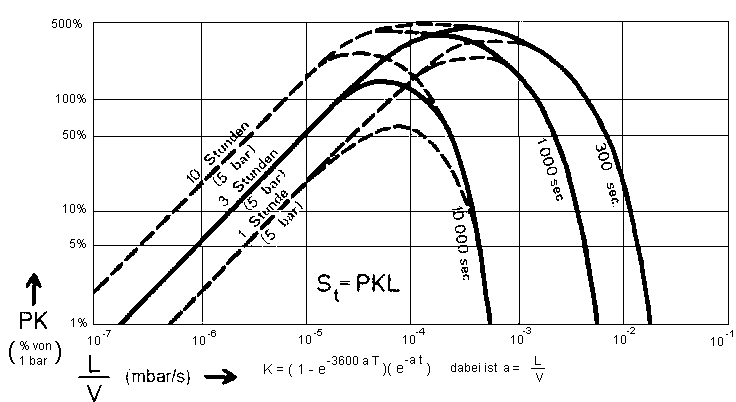

Die Anwendung dieser Kurven kann gut am Beispiel 2 illustriert werden. Das Verhältnis L/V ist dort 10^-5 mbar/sec

Wenn man nun die L/V-Teilungslinie von 10^-5 nach oben verfolgt, so schneidet sie die Kurve (Beispiel 2 - Bombingzeit 3 Std.) bei 51%. Damit ist die angezeigte Leckrate 51% von 1 x 10^-8 nämlich 5,1 x 10^-9 mbar l/s. Man beachte, dass dies unabhängig von der Wartezeit ist, zumindest bis 10.00 Sekunden.

Dieser Prozentsatz würde auch für jedes andere Testobjekt gelten, geprüft unter diesen Bedingungen, vorausgesetzt es hat ein L/V-Verhältnis von 10^-5 mbar/s . Zum Beispiel trifft es auch zu für ein Prüfobjekt mit dem internen Volumen von 10² cm³und einer Leckrate von 1 x 10^-7 mbar l/s. Hier wäre die angezeigte Leckrate 51% von 1 x 10^-7, nämlich 5,1 x 10^-8 mbar·l/s.

Dies gilt also auch für das Beispiel 3 mit L = 10^-5 mbar l/s und V = 1 cm^-3. Wieder ist hier das Verhältnis L/V = 10^-5 mbar/s und damit der Füllgrad 51% und auch die angezeigte Leckrate 51% von 10^-5 mbar  l/s = 5,1 x 10^-6 mbar l/s.

Noch interessanter ist das Beispiel 1. Hier ist die Leckrate 1 x 10^-5 mbar l/s und das Volumen 10^-3 cm³. Damit ist L/V = 10² mbar/s. Nach einer Wartezeit von 300 Sekunden ist die Spürgasfüllung auf rund 20% abgefallen und damit die angezeigte Leckrate 20% von 1 x 10^-5 = 2 x 10^-6 mbar l/s - wenn der Test 300 Sekunden nach der Entnahme durchgeführt wird. Der Verlust an Spürgas geschieht hier sehr schnell. Nicht erkennbar in dieser Darstellung ist, dass dennoch nach einer Wartezeit von 1000 Sekunden (17 Minuten) die 10^-5 sec^-1-Linie noch 0,02% aufweist und damit eine Leckrate von 2 x 10^-9 angezeigt wird.

Um zu zeigen, wie eng der Zusammenhang zwischen St und L ist, zeigt der folgende Auszug aus den Tabellen. Dieser Auszug umfasst zwei Volumina, 10^-3 und 10^-2 cm³ (womit die meisten hermetisch geschlossenen, elektronischen Bauteile erfasst sind), und die wahren Leckraten von 10^-5 bis 10^-7 mbar l/s. Starke Anhaltspunkte zeigen, dass buchstäblich alle Lecks (L) an Glas-zu-Metall-, Keramik-zu-Metall-Verbindungen etc. Leckraten von 5 x 10^-7 Std·cm³/s oder größer haben. Die Zahlen dieser Tabelle sind ein Auszug aus der 14-seitigen Originaltabelle, wobei der Bombingdruck auf 5 bar festgelegt wurde. Auch ist diese Tabelle zum schnelleren Ablesen neu geordnet.

Es ist bedeutsam, dass die Werte der angezeigten Leckraten innerhalb einer halben Größenordnung zur wahren Leckrate liegen, für alle Werte außer denen der ersten Kolonne. Dort ist es notwendig, innerhalb einer Wartezeit von 300 bis 1000 Sekunden zu testen, um Ergebnisse zu erhalten, die vernünftig nahe zur wahren Leckrate liegen. Damit liefert diese Tabelle einen guten Überblick, warum die Resultate der Dichtheitsmessungen mit der Bombing- Technik an geschlossenen Bauteilen sinnvolle Aussagen ermöglichen

W.E. Briggs
S.G Burnett
Oktober 1968